Wyznacz wartości 𝑎 takie, że prosta![]()
![]()
Naszkicuj rysunek pomocniczy:
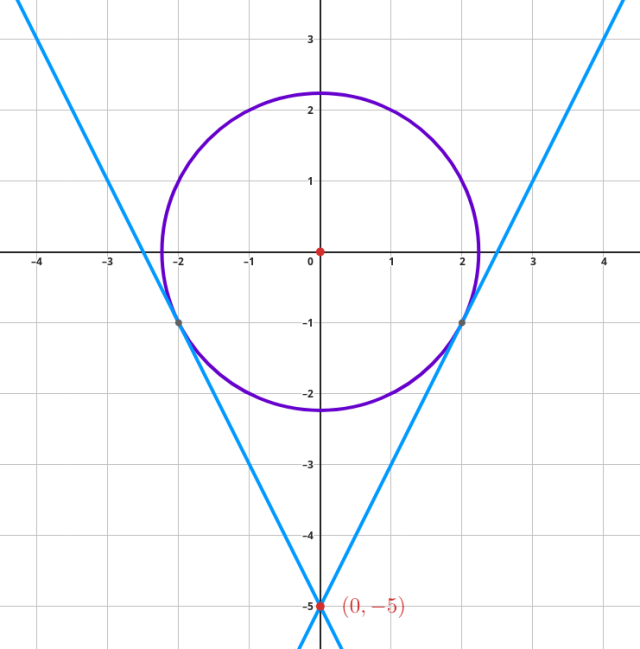
Ułóż układ równań:
![]()
Podstaw równanie kierunkowe prostej do równania okręgu:
![]()
![]()
![]()
Oblicz wyróżnik tego równania:
![]()
![]()
![]()
Równanie ma dwa rozwiązania (czyli prosta przecina okrąg), gdy wyróżnik jest większy od zera:
![]()
![]()
![]()
![]()

Ułóż układ równań z równania okręgu oraz prostej podanej w zadaniu. Podstaw wzór w postaci kierunkowej do równania okręgu. Przekształć wyrażenie do postaci wielomianu stopnia drugiego z parametrem 𝑎. Oblicz wyróżnik tego wielomianu. Jako że rozwiązaniem mają być proste przecinające okrąg (czyli dzielące dwa punkty wspólne z okręgiem), ustaw ten wyróżnik większy zeru. Podaj zbiór wartości 𝑎, dla których wyróżnik jest większy od zera.

Ćwiczenie B.
217Ćwiczenie C.
218Zadanie 1.
220Zadanie 2.
220Zadanie 6.
220Zadanie 9.
221Zadanie 12.
221Zadanie 14.
221Zadanie 15.
221Zadanie 17.
221Zadanie 18.
222Zadanie 20.
222Zadanie 21.
222Ćwiczenie A.
223Ćwiczenie B.
224Przykład 2.
226Zadanie 1.
228Zadanie 2.
228Zadanie 4.
228Zadanie 5.
228Zadanie 7.
228Zadanie 8.
228Zadanie 9.
228Zadanie 11.
229Zadanie 12.
229Zadanie 14.
229Zadanie 15.
229Zadanie 16.
229Zadanie 1.
234Zadanie 3.
234Zadanie 4.
234Zadanie 6.
234Zadanie 7.
234Zadanie 8.
234Zadanie 9.
234Zadanie 13.
235Zadanie 15.
235Ćwiczenie B.
236Ćwiczenie C.
237Zadanie 1.
238Zadanie 3.
238Zadanie 4.
239Zadanie 5.
239Zadanie 6.
239Zadanie 8.
239Zadanie 9.
239Zadanie 10.
239Zadanie 11.
239Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 2.
245Zadanie 5.
247Zadanie 6.
247Zadanie 7.
247Zadanie 8.
247Zadanie 11.
247Zadanie 12.
247Zadanie 15.
248Zadanie 16.
248Zadanie 17.
248Zadanie 18.
248Zadanie 1.
250Zadanie 7.
250Zadanie 8.
250
