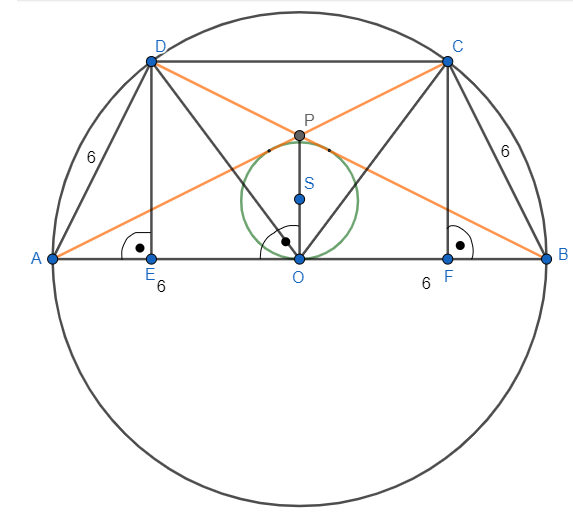
Trapez równoramienny ABCD o ramieniu długości 6, gdzie dłuższa podstawa AB ma długość 12 i jest średnicą wpisanego okręgu przekątne AC i BD przecinają się w punkcie P. Musisz obliczyć pole koła wpisanego w trójkąt ABP.
![]()
Z tw Pitagorasa
![]()
![]()
![]()
![]()
![]()
OD i OC – promienie okręgu opisanego na trapezie ABCD
![]()
![]()
![]()
Z tw Pitagorasa
![]()
![]()
![]()
![]()
![]()
![]()
Trójkąt BP i trójkąt CDP są podobne
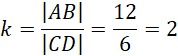
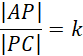
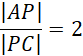
![]()
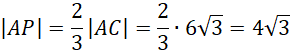
Z tw Pitagorasa
![]()
![]()
![]()
![]()
![]()
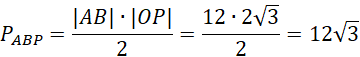
![]()
![]()
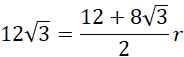
![]()
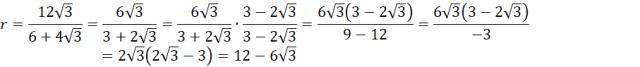
![]()

Przyjmij oznaczenia jak na rysunku. AB jest średnicą okręgu, więc kąty oparte na tej średnicy to kąty proste. Z twierdzenia Pitagorasa wyznacz długość |AC|. Wykorzystaj fakt, że trójkąty AOD i OBC są równoboczne. Kolejno oblicz długość |ED| z twierdzenia Pitagorasa. Zauważ, że trójkąty ABP i CDP są podobne z cechy kkk. Oblicz skalę ich podobieństwa. Następnie oblicz długość odcinka AP. Kolejno oblicz długość |OP| z twierdzenia Pitagorasa. Oblicz pole trójkąta ABP. Kolejno wyznacz obwód trójkąta ABP. W następnej kolejności wyznacz długość promienia okręgu wpisanego w trójkąt ABP. Na koniec oblicz pole koła wpisanego w trójkąt ABP.

Zadanie 1.
93Zadanie 2.
93Zadanie 3.
94Zadanie 4.
94Zadanie 5.
94Zadanie 6.
94Zadanie 7.
95Zadanie 8.
95Zadanie 9.
95Zadanie 10.
95Zadanie 11.
95Zadanie 12.
96Zadanie 13.
96Zadanie 20.
97Zadanie 26.
97Zadanie 28.
98Zadanie 29.
98Zadanie 30.
98Zadanie 31.
98Zadanie 32.
99Zadanie 33.
99Zadanie 34.
99Zadanie 37.
100Zadanie 38.
100Zadanie 39.
100Zadanie 40.
100Zadanie 42.
100Zadanie 43.
101Zadanie 44.
101Zadanie 45.
101Zadanie 46.
102Zadanie 47.
102Zadanie 48.
102Zadanie 50.
102Zadanie 51.
102Zadanie 54.
103Zadanie 55.
103Zadanie 56.
103Zadanie 64.
104Zadanie 66.
105Zadanie 67.
105Zadanie 75.
106Zadanie 78.
106Zadanie 82.
107Zadanie 83.
107Zadanie 84.
107Zadanie 87.
108Zadanie 88.
108Zadanie 89.
108Zadanie 90.
108Zadanie 94.
109Zadanie 95.
109Zadanie 99.
110Zadanie 102.
110Zadanie 103.
110Zadanie 8.
112Zadanie 10.
113
