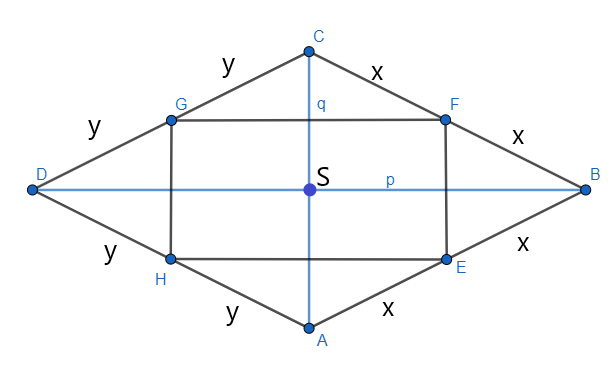
W deltoidzie, który jest przedstawiony na rysunku obok, połączono ze sobą środki boków. Musisz obliczyć obwód otrzymanego czworokąta.
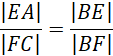
![]()
Proste EF i AC są równoległe
Proste HG i AC są równoległe
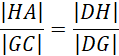
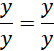
Proste EF i HG są równoległe
Proste EH i FG są równoległe
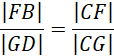
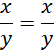
Proste BD i FG są równoległe
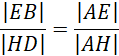
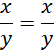
Proste EH i BD są równoległe
Proste EH i FG są równoległe
Przekątne w deltoidzie przecinają się pod kątem prostym
![]()
![]()
![]()
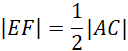
![]()
![]()
Z tw cosinusów
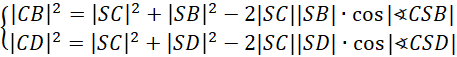
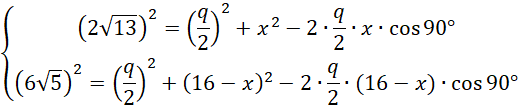
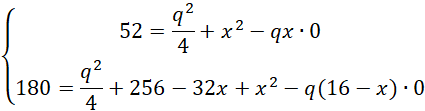
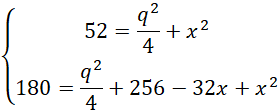
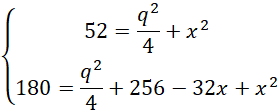
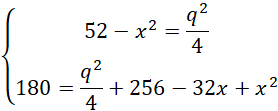
![]()
![]()
![]()
![]()
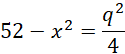
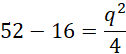
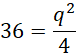
![]()
![]()
![]()
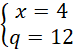
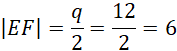
![]()

Przyjmij oznaczenia jak na rysunku powyżej. Skorzystaj z twierdzenia odwrotnego do twierdzenia Talesa, aby pokazać, że proste EF i AC, HG i AC, EF i HG, EH i FG, FG i BD, EH i BD, EH i FG są parami równoległymi. Czworokąt EFGH jest prostokątem, ponieważ w deltoidzie przekątne przecinają się pod kątem prostym. Wykorzystaj fakt, że odcinek łączący środki ramion trapezu jest równy średniej arytmetycznej długości podstaw. Przyjmij oznaczenia jak powyżej i skorzystaj z twierdzenia cosinusów i oblicz q i x. Wyznacz długość drugiego boku prostokąta EFGH i na koniec obwód prostokąta EFGH.

Zadanie 1.
93Zadanie 2.
93Zadanie 3.
94Zadanie 4.
94Zadanie 5.
94Zadanie 6.
94Zadanie 7.
95Zadanie 8.
95Zadanie 9.
95Zadanie 10.
95Zadanie 11.
95Zadanie 12.
96Zadanie 13.
96Zadanie 20.
97Zadanie 26.
97Zadanie 28.
98Zadanie 29.
98Zadanie 30.
98Zadanie 31.
98Zadanie 32.
99Zadanie 33.
99Zadanie 34.
99Zadanie 37.
100Zadanie 38.
100Zadanie 39.
100Zadanie 40.
100Zadanie 42.
100Zadanie 43.
101Zadanie 44.
101Zadanie 45.
101Zadanie 46.
102Zadanie 47.
102Zadanie 48.
102Zadanie 50.
102Zadanie 51.
102Zadanie 54.
103Zadanie 55.
103Zadanie 56.
103Zadanie 64.
104Zadanie 66.
105Zadanie 67.
105Zadanie 75.
106Zadanie 78.
106Zadanie 82.
107Zadanie 83.
107Zadanie 84.
107Zadanie 87.
108Zadanie 88.
108Zadanie 89.
108Zadanie 90.
108Zadanie 94.
109Zadanie 95.
109Zadanie 99.
110Zadanie 102.
110Zadanie 103.
110Zadanie 8.
112Zadanie 10.
113
