Przekątne pięciokąta foremnego ABCDE o boku długości "a" tworzą wewnętrznie mniejszy pięciokąt foremny FGHIJ. Wykaż, że punkt J dzieli odcinek AD w złotym stosunku, tzn. że ![]()
![]()
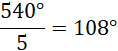
![]()
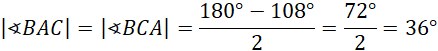
![]()
![]()
![]()
![]()
![]()
![]()
Dlatego
![]()
![]()
![]()
Czyli
![]()
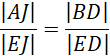
Czyli
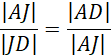

Zacznij od wyznaczenia sumy miar kątów wewnętrznych w pięciokącie. Kolejno wyznacz miarę kąta wewnętrznego w pięciokącie foremnym. Wiadomo, że trójkąt CBA jest równoramienny. Wyznacz miary kątów BAC i BCA. Wiadomo, że kąty BAC i EAD mają takie same miary. Następnie wykorzystaj fakt, że trójkąt AFE jest równoramienny i wskaż, że kąty AEF i FAE są równe. Kolejno wyznacz miarę kąta AFE i następnie miarę kąta EFD. Wykorzystaj fakt, że trójkąt FJE jest równoramienny i wskaż, że kąty FJE i JFE są równe. Wyznacz miarę kąta FEJ. Wiadomo, że trójkąt AJE jest równoramienny, czyli boki AJ i AE są równe i mają długość a. Trójkąt BDE jest równoramienny, ponieważ przekątne w pięciokącie mają taką samą długość. Wyznacz miarę kąta BED. Trójkąty AJE i BDE mają identyczne miary, więc są one podobne z cechy kkk. Z podobieństwa tych trójkątów wyznacz równość ![]()
![]()

Zadanie 1.
93Zadanie 2.
93Zadanie 3.
94Zadanie 4.
94Zadanie 5.
94Zadanie 6.
94Zadanie 7.
95Zadanie 8.
95Zadanie 9.
95Zadanie 10.
95Zadanie 11.
95Zadanie 12.
96Zadanie 13.
96Zadanie 20.
97Zadanie 26.
97Zadanie 28.
98Zadanie 29.
98Zadanie 30.
98Zadanie 31.
98Zadanie 32.
99Zadanie 33.
99Zadanie 34.
99Zadanie 37.
100Zadanie 38.
100Zadanie 39.
100Zadanie 40.
100Zadanie 42.
100Zadanie 43.
101Zadanie 44.
101Zadanie 45.
101Zadanie 46.
102Zadanie 47.
102Zadanie 48.
102Zadanie 50.
102Zadanie 51.
102Zadanie 54.
103Zadanie 55.
103Zadanie 56.
103Zadanie 64.
104Zadanie 66.
105Zadanie 67.
105Zadanie 75.
106Zadanie 78.
106Zadanie 82.
107Zadanie 83.
107Zadanie 84.
107Zadanie 87.
108Zadanie 88.
108Zadanie 89.
108Zadanie 90.
108Zadanie 94.
109Zadanie 95.
109Zadanie 99.
110Zadanie 102.
110Zadanie 103.
110Zadanie 8.
112Zadanie 10.
113
