W prostokącie ABCD wybrano punkt E na boku CD tak, że |EC| = 2|DE|, oraz punkt F na boku AB tak, że |BF| = |DE|. Punkt przecięcia prostych EF i BC oznaczmy jako P. Udowodnij, że trójkąty AED i FPB są przystające.
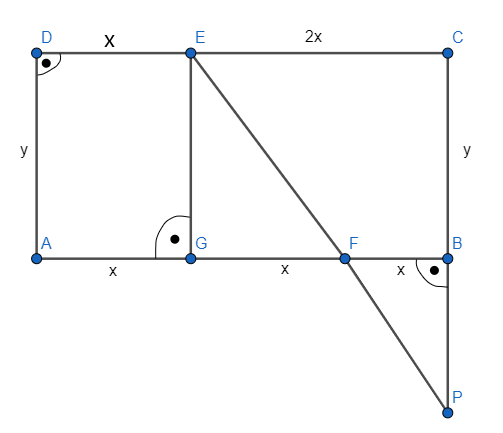
Trójkąty ADE i EGF są przystające
![]()
Trójkąty EGF i PBF są przystające
Wynika z tego, że trójkąty ADE i PBF są przystające
![]()

Stwórz rysunek pomocniczy. Trójkąt ADE i trójkąt EGF są przystające z cechy bkb. Trójkąt EGF i trójkąt PBF są przystające na podstawie cechy kbk – dwa kąty mają taka samą miarę, a krótsze przyprostokątne obu trójkątów mają długość x. Skoro trójkąty ADE i EGF oraz EGF i PBF są przystające to trójkąty ADE i PBF są przystające.

Zadanie 1.
93Zadanie 2.
93Zadanie 3.
94Zadanie 4.
94Zadanie 5.
94Zadanie 6.
94Zadanie 7.
95Zadanie 8.
95Zadanie 9.
95Zadanie 10.
95Zadanie 11.
95Zadanie 12.
96Zadanie 13.
96Zadanie 20.
97Zadanie 26.
97Zadanie 28.
98Zadanie 29.
98Zadanie 30.
98Zadanie 31.
98Zadanie 32.
99Zadanie 33.
99Zadanie 34.
99Zadanie 37.
100Zadanie 38.
100Zadanie 39.
100Zadanie 40.
100Zadanie 42.
100Zadanie 43.
101Zadanie 44.
101Zadanie 45.
101Zadanie 46.
102Zadanie 47.
102Zadanie 48.
102Zadanie 50.
102Zadanie 51.
102Zadanie 54.
103Zadanie 55.
103Zadanie 56.
103Zadanie 64.
104Zadanie 66.
105Zadanie 67.
105Zadanie 75.
106Zadanie 78.
106Zadanie 82.
107Zadanie 83.
107Zadanie 84.
107Zadanie 87.
108Zadanie 88.
108Zadanie 89.
108Zadanie 90.
108Zadanie 94.
109Zadanie 95.
109Zadanie 99.
110Zadanie 102.
110Zadanie 103.
110Zadanie 8.
112Zadanie 10.
113
