Bez wyznaczania miar kątów trójkąta rozstrzygnij, który bok trójkąta jest najkrótszy, a który najdłuższy, jeśli:
oraz w trójkącie ostrokątnym ABC naprzeciw boków długości a, b, c leżą odpowiednio kąty
.
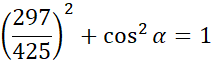
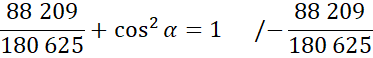
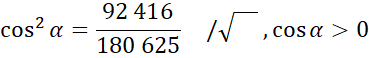
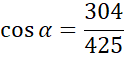
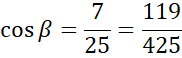
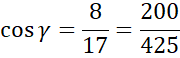
Najdłuższy bok:
, najkrótszy bok:
.
Skorzystaj z jedynki trygonometrycznej i wyznacz wartość cosinusa kąta
wstawiając w miejsce sinusa jego podaną wartość.
Zauważ, że dla kąta ostrego wartość cosinusa maleje wraz ze wzrostem miary kąta, więc największy kąt będzie przyjmowany dla najmniejszej wartości cosinusa. Doprowadź podane ułamki do wspólnego mianownika i porównaj ze sobą.
Na koniec skorzystaj z tego, że najdłuższy bok trójkąta leży naprzeciwko największego kąta, a najkrótszy naprzeciwko najmniejszego.