Należy znaleźć prostokąt o największym polu przy obwodzie równym 30.
30 = 7.5 · 4

Obwód prostokąta można wyrazić jako:
30 = 2a + 2b
15 = a + b
a = 15 – b
Funkcja optymalizacyjna to:
f(b) = b · (15 – b)
Miejsca zerowe:
b · (15 – b) = 0
b = 0 lub b = 15
Funkcja przyjmuje największą wartość w wierzchołku, ponieważ ramiona paraboli są skierowane w dół, więc:
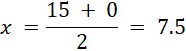
![]()
![]()

Ćwiczenie 2.
394Ćwiczenie 3.
394Zadanie 1.
394Zadanie 2.
395Zadanie 3.
395Zadanie 4.
395Zadanie 15.
396Zadanie 17.
396Ćwiczenie 1.
397Ćwiczenie 2.
398Ćwiczenie 3.
398Ćwiczenie 4.
399Zadanie 1.
401Zadanie 2.
401Zadanie 3.
401Zadanie 4.
401Zadanie 6.
402Zadanie 7.
402Zadanie 8.
402Zadanie 9.
402Zadanie 1.
408Zadanie 2.
408Zadanie 1.
413Zadanie 2.
414Zadanie 3.
414Zadanie 4.
414Zadanie 6.
414Zadanie 7.
414Zadanie 1.
422Zadanie zestaw 1 7.
424Zadanie zestaw 2 7.
426Zadanie zestaw 2 9.
426
