Oblicz obwód równoległoboku R₂, jeśli jego pole jest równe i jest on podobny do równoległoboku którego boki mają długości 4 cm i 6 cm, a jedna z przekątnych tego równoległoboku jest prostopadła do jego krótszych boków.

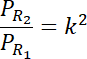
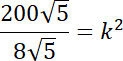
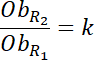
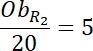
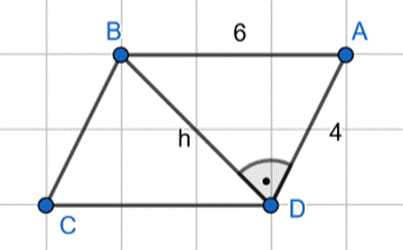
Skorzystaj z twierdzenia Pitagorasa w trójkącie ABD i na tej podstawie oblicz długość wysokość tego równoległoboku opadającej na krótszą podstawę.

A następnie oblicz obwód i pole powstałego równoległoboku.

Skorzystaj z tego, że równoległoboki R₂ i R₁ są podobne i na tej podstawie zapisz stosunek ich pól. Zauważ, że jeśli skala podobieństwa dwóch figur wynosi , to stosunek ich pól jest równy .

Pod powstałe równanie podstaw znane wartości i z powstałego równania wyznacz wartość , czyli skalę podobieństwa tych figur.

Skorzystaj z tego, że znasz skalę podobieństwa figur R₁ i R­₂. Więc ich obwody będą podobne w takiej samej skali. Pod powstałe równanie podstaw znane wartości i wyznacz z niego obwód równoległoboku R₂.