Matematyka z plusem. Klasa 2. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Podręcznik, Wydawnictwo: GWO

Zadanie 7, c) - strona 46

W tym zadaniu znajdź rozwiązania równań.

Korzystasz z twierdzenia o rozwiązaniach całkowitych i podstawiasz za x dzielniki wyrazu wolnego wielomianu w poszukiwaniu jego pierwiastków.

$\text{[math]}$

$\text{[math]}$

Zatem liczba 1 jest pierwiastkiem W(x).

$\text{[math]}$

$\text{[math]}$

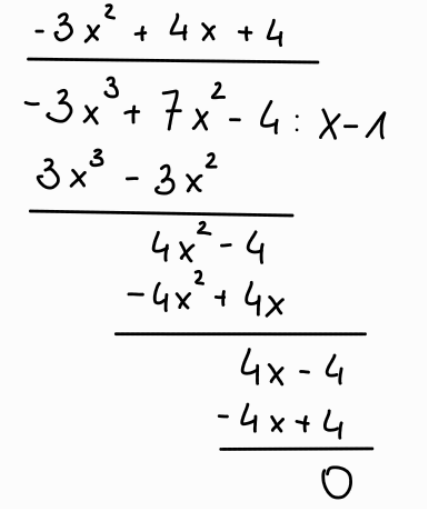
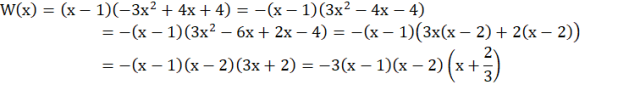
Zgodnie z twierdzeniami o pierwiastkach całkowitych wielomianu sprawdzasz, które liczby są jego pierwiastkami. Po ustaleniu danej liczby wykonujesz dzielenie pisemne wielomianu. Wynikiem dzielenia jest trójmian kwadratowy, który sprowadzasz do najprostszej postaci, co umożliwi ustalenie wszystkich pierwiastków wielomianu.

Zadanie 19., strona 191, Matematyka. Klasa 4. Podręcznik – rozwiązania i odpowiedzi

Ćwiczenie Ćwiczenie 5., strona 122, Matematyka wokół nas. Klasa 7. Podręcznik - rozwiązania i odpowiedzi

Zadanie 6., strona 378, Prosto do matury. Matematyka. Klasa 1. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 5.49., strona 130, Matematyka. Klasa 3. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 1, strona 241, Matematyka wokół nas. Klasa 6. Podręcznik – rozwiązania i odpowiedzi

Zadanie 13, strona 256, Matematyka z kluczem. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie 15., strona 218, Matematyka. Klasa 2. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 78., strona 188, Prosto do matury. Klasa 3. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie 1., strona 129, Matematyka z Plusem. Klasa 4. Podręcznik – rozwiązania i odpowiedzi

Zadanie 1, strona 9, Matematyka. Klasa 8. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

10

Ćwiczenie B

11

11

11

11

Przykład 1

11

11

11

11

Przykład 2

12

12

12

12

Zadanie 1

13

13

13

13

Zadanie 2

13

13

13

13

13

Zadanie 3

13

13

13

13

13

13

13

13

13

13

13

13

13

Zadanie 4

13

13

13

13

Zadanie 5

13

13

13

13

13

13

13

Zadanie 6

13

13

13

13

13

Zadanie 7

14

14

14

Zadanie 8

14

14

14

14

14

14

Zadanie 9

14

14

14

Zadanie 10

14

14

14

Zadanie 11

14

14

14

14

14

14

14

14

Zadanie 13

14

14

14

15

15

15

Ćwiczenie A

15

15

15

17

Przykład 1

15

15

15

Przykład 2

16

16

16

Przykład 3

17

17

17

17

Przykład 4

18

18

18

18

Zadanie 1

19

19

19

19

19

19

19

Zadanie 2

19

19

19

19

19

19

19

Zadanie 3

19

19

19

19

19

19

19

Zadanie 4

19

19

19

19

19

19

19

Zadanie 5

19

19

19

19

19

19

19

Zadanie 6

20

20

20

20

20

20

20

20

20

20

20

20

20

Zadanie 7

20

20

20

20

20

20

Zadanie 8

20

20

20

20

20

20

20

Zadanie 9

20

20

20

20

20

20

20

Zadanie 10

20

20

20

20

Zadanie 11

20

20

20

20

Zadanie 12

20

20

20

20

Zadanie 13

21

21

21

21

21

Zadanie 14

21

21

21

21

21

21

21

Zadanie 15

21

21

21

21

21

21

21

21

21

Zadanie 16

21

21

21

21

21

21

21

21

Ćwiczenie A

22

22

22

Ćwiczenie B

22

22

22

22

Ćwiczenie C

25

25

25

25

26

Ćwiczenie F

26

26

26

26

26

Przykład 1

23

23

23

23

Przykład 2

24

24

24

24

Zadanie 1

26

26

26

26

26

26

26

Zadanie 2

26

26

26

26

Zadanie 3

26

26

26

26

26

26

26

Zadanie 4

27

27

27

27

27

27

27

27

27

Zadanie 5

27

27

27

27

27

Zadanie 6

27

27

27

27

27

27

27

Zadanie 7

27

27

27

27

27

27

27

27

27

27

Zadanie 8

27

27

27

27

27

27

27

27

27

27

Zadanie 9

27

27

27

27

Zadanie 10

27

27

27

27

27

27

27

27

27

27

Zadanie 11

28

28

28

28

28

Zadanie 12

28

28

28

28

28

28

28

Zadanie 13

28

28

28

28

Zadanie 14

28

28

28

28

28

28

Zadanie 17

28

28

28

28

28

Zadanie 18

28

28

28

28

28

28

28

Zadanie 19

28

28

28

28

Zadanie 20

29

29

29

29

29

Zadanie 21

29

29

29

29

29

29

Zadanie 23

29

29

29

29

29

29

29

29

Ćwiczenie A

30

30

30

31

32

33

Zadanie 1

33

33

33

Zadanie 2

33

33

33

33

33

33

33

Zadanie 3

33

33

33

33

33

Zadanie 4

34

34

34

34

34

Zadanie 5

34

34

34

Zadanie 6

34

34

34

34

34

34

34

Zadanie 7

34

34

34

34

Zadanie 9

34

34

34

Zadanie 10

34

34

34

35

Zadanie 12

36

36

36

36

36

36

36

36

36

36

36

37

37

38

Zadanie 1

39

39

39

39

39

Zadanie 2

39

39

39

Zadanie 3

39

39

39

Zadanie 4

39

39

39

Zadanie 5

39

39

39

39

39

39

39

40

Zadanie 7

40

40

40

40

40

40

40

40

40

42

43

45

44

Zadanie 1

45

45

45

45

45

Zadanie 2

45

45

45

45

45

45

45

Zadanie 3

45

45

45

Zadanie 4

45

45

45

45

45

Zadanie 5

45

45

45

45

45

45

45

Zadanie 6

46

46

46

46

46

46

46

46

46

Zadanie 7

46

46

46

46

46

46

46

Zadanie 8

46

46

46

46

46

46

46

Zadanie 9

46

46

46

46

46

46

46

46

46

46

Zadanie 13

46

46

46

46

47

47

Zadanie 16

47

47

47

47

47

47

47

47

47

47

Zadanie 1

48

48

48

Zadanie 2

48

48

48

48

Zadanie 4

48

48

48

48

48

48

48

48

Zadanie 6

48

48

48

48

48

48

Zadanie 8

48

48

48

48

Zadanie 9

48

48

48

Zadanie 10

48

48

48

48

48

Zadanie 13

48

48

48

48

Pełny spis treści