Zbiór zadań, Wydawnictwo: Nowa Era

Zadanie 7. - strona 43

W tym zadaniu należy określić liczbę rozwiązań równania $\text{[math]}$ , które należą do przedziału $\text{[math]}$ .

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

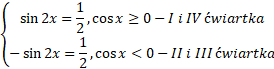
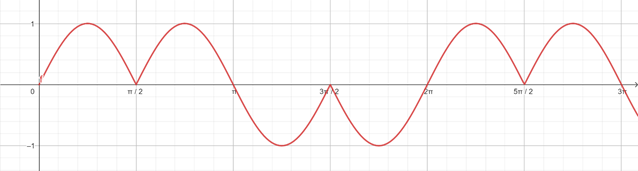
4 rozwiązania na okres podstawowy $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

3

4

4

Naszkicuj wykres funkcji w dwóch przypadkach – w pierwszym cosinus jest nieujemny, czyli rysujemy go w I i IV ćwiartce, a w drugim przypadku cosinus jest ujemny – II i III ćwiartka. Zauważ, że na jeden pełny okres podstawowy funkcja ma 4 rozwiązania. Podziel największą liczbę z przedziału przez okres podstawowy, aby ustalić ilość pełnych cykli. Pomnóż tę ilość przez rozwiązania przypadające na jeden cykl.

Zadanie 32., strona 63, Teraz matura. Klasa 4. Poziom rozszerzony. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 2, strona 109, Matematyka. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie 29., strona 114, Matematyka. Klasa 8. Zbiór zadań - rozwiązania i odpowiedzi

Ćwiczenie 1., strona 131, Matematyka. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie 8.9., strona 60, Prosto do matury. Matematyka. Klasa 2. Podręcznik. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Zadanie 5.65, strona 143, Matematyka. Klasa 1. Zakres podstawowy. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 24., strona 85, Matematyka z kluczem. Klasa 7. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 11, strona 61, Matematyka z kluczem. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie 8., strona 19, Matematyka z kluczem. Klasa 6. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

Zadanie 5, strona 167, Matematyka z kluczem. Klasa 6. Zbiór zadań - rozwiązania i odpowiedzi

38

Zadanie 2.

38

38

38

38

Zadanie 3.

38

38

38

38

38

38

38

38

38

38

Zadanie 5.

38

38

38

38

38

38

38

38

38

Zadanie 6.

38

38

38

38

38

Zadanie 7.

38

38

38

38

38

38

38

Zadanie 8.

38

38

38

38

38

38

38

Zadanie 9.

39

39

39

39

39

Zadanie 10.

39

39

39

39

39

Zadanie 11.

39

39

39

39

39

Zadanie 12.

39

39

39

39

39

39

39

Zadanie 13.

39

39

39

39

Zadanie 14.

39

39

39

Zadanie 15.

39

39

39

39

39

Zadanie 16.

40

40

40

40

40

40

40

40

40

Zadanie 17.

40

40

40

40

40

40

40

Zadanie 18.

40

40

40

40

Zadanie 19.

40

40

40

40

40

40

40

Zadanie 20.

40

40

40

40

40

40

40

40

40

Zadanie 21.

40

40

40

40

40

Zadanie 22.

40

40

40

40

40

40

40

Zadanie 23.

41

41

41

41

41

Zadanie 24.

41

41

41

41

41

41

41

Zadanie 25.

41

41

41

41

41

41

41

41

41

41

Zadanie 26.

41

41

41

41

41

41

41

Zadanie 27.

41

41

41

41

41

Zadanie 28.

41

41

41

41

Zadanie 29.

41

41

41

41

Zadanie 30.

41

41

41

41

42

42

42

42

42

42

42

42

42

43

43

43

43

43

43

43

43

44

44

44

44

44

44

44

44

44

44

44

44

45

45

45

45

45

45

Zadanie 19.

45

45

45

45

45

45

46

46

46

46

46

46

46

46

46

46

46

46

46

Pełny spis treści