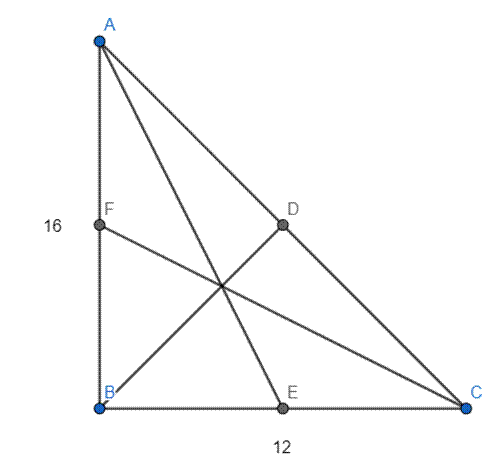
Oblicz odległość środka ciężkości tego trójkąta od wierzchołka kąta prostego.
![]()
![]()
![]()
|AC| = 20
![]()
![]()

Środek ciężkości trójkąta to miejsce przecięcia się środkowych. Środkowe przecinają się w środku ciężkości trójkąta, który dzieli środkową na dwa odcinki pozostając ze sobą w stosunku 2 : 1. Najpierw skorzystaj z twierdzenia Pitagorasa w trójkącie ABC, aby obliczyć długość odcinka AC. |BD| jest równa połowie odległości |AC| i długości promienia okręgu opisanego na tym trójkącie. Odległość środka ciężkości tego trójkąta od wierzchołka kąta prostego jest równa
![]() .
.

Zadanie 7.4
164Zadanie 7.5
164Zadanie 7.9
165Zadanie 7.12
165Zadanie 7.15
165Zadanie 7.16
166Zadanie 7.19
166Zadanie 7.21
166Zadanie 7.22
167Zadanie 7.25
167Zadanie 7.27
167Zadanie 7.29
168Zadanie 7.30
168Zadanie 7.31
168Zadanie 7.36
169Zadanie 7.37
169Zadanie 7.38
169Zadanie 7.41
170Zadanie 7.42
170Zadanie 7.46
170Zadanie 7.47
170Zadanie 7.48
171Zadanie 7.49
171Zadanie 7.51
172Zadanie 7.52
172Zadanie 7.53
172Zadanie 7.64
173Zadanie 7.65
173Zadanie 7.83
175Zadanie 7.84
175Zadanie 7.91
176Zadanie 7.93
176Zadanie 7.94
176Zadanie 7.95
176Zadanie 7.97
177Zadanie 7.101
177Zadanie 7.127
180Zadanie 7.128
181Zadanie 7.129
181Zadanie 7.130
182Zadanie 7.133
183Zadanie 7.134
183Zadanie 7.135
183Zadanie 7.150
184Zadanie 25.
188Zadanie 29.
188Zadanie 34.
188Zadanie 38.
188
