W tym zadaniu należy obliczyć opór drugiego odbiornika.
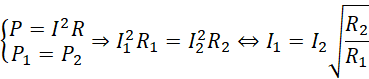
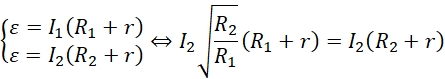
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Z równości mocy i ich definicyjnego przedstawienia za pomocą iloczynu kwadratu natężenia i oporu, należało uzależnić jedno natężenie od drugiego:
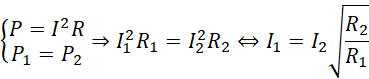
Następnie należało skorzystać z prawa Ohma dla całego obwodu i zauważyć, że siły SEM są takie same, następnie wstawić za natężenie pierwsze zależność od natężenia drugiego i stworzyć równanie:
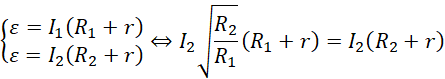
Rozwiązaniem równania ze względu na R2 jest
![]()
Drugie rozwiązanie to opór, który już znamy.

Ćwiczenie 2.4
25Ćwiczenie 2.8
26Ćwiczenie 3.1
27Ćwiczenie 3.2
28Ćwiczenie 3.7
29Ćwiczenie 3.8
29Ćwiczenie 3.11
29Ćwiczenie 3.12
30Ćwiczenie 3.13
30Ćwiczenie 3.14
30Ćwiczenie 3.15
31Ćwiczenie 3.16
31Ćwiczenie 3.17
32Ćwiczenie 3.19
33Ćwiczenie 3.20
33Ćwiczenie 3.21
33Ćwiczenie 5.7
36Ćwiczenie 5.8
37Ćwiczenie 5.9
37Ćwiczenie 5.10
37Ćwiczenie 5.12
37Ćwiczenie 5.13
38Ćwiczenie 6.7
39Ćwiczenie 6.10
40Ćwiczenie 6.12
40Ćwiczenie 7.4
42Ćwiczenie 7.5
42Ćwiczenie 7.6
42Ćwiczenie 8.4
44Ćwiczenie 8.5
44Ćwiczenie 8.6
45Ćwiczenie 8.7
45Ćwiczenie 8.8
45Ćwiczenie 9.1
45Ćwiczenie 9.3
46Ćwiczenie 9.4
46Ćwiczenie 9.5
47Ćwiczenie 9.6
47Ćwiczenie 9.7
48Ćwiczenie 9.8
48Ćwiczenie 9.9
48Ćwiczenie 10.2
49Ćwiczenie 10.4
49Ćwiczenie 10.6
50Ćwiczenie 11.3
52Ćwiczenie 11.4
52Ćwiczenie 11.5
52Ćwiczenie 12.2
54Ćwiczenie 12.4
55
