Fizyka. Klasa 3. Zakres rozszerzony. Zbiór zadań - rozwiązania i odpowiedzi

Zbiór zadań, Wydawnictwo: WSiP

Ćwiczenie 5.8, a) - strona 37

W tym zadaniu należy obliczyć moc, która wydzieliła się w całym obwodzie.

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

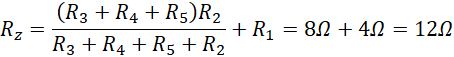
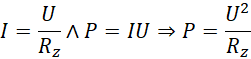
Pierwszym krokiem do rozwiązania tego zadania jest policzenie oporu zastępczego całego obwodu, gdzie wyraźnie widać, że oporniki 3, 4, 5 są szeregowe i ich układ jest równoległy do opornika 2, ten zaś równoległy układ jest szeregowy do opornika 1, stąd:

$\text{[math]}$

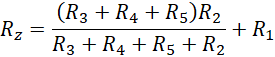
Następnie wystarczy wyjść z prawa Ohma i definicji mocy prądu elektrycznego:

$\text{[math]}$

Zadanie 7.60., strona 105, Fizyka. Klasa 7-8. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 4.4., strona 158, Zrozumieć fizykę. Klasa 1. Zakres rozszerzony. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 3.2., strona 107, Zrozumieć fizykę. Klasa 1. Zakres rozszerzony. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 14., strona 199, Odkryć fizykę. Klasa 2. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 6, strona 101, Fizyka. Klasy 1-3. Zakres podstawowy. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 5.91., strona 73, Fizyka. Klasa 7-8. Zbiór zadań - rozwiązania i odpowiedzi

Ćwiczenie 1., strona 28, Fizyka. Klasa 7. Zeszyt ćwiczeń – rozwiązania i odpowiedzi

Zadanie 19.7, strona 290, Zrozumieć fizykę 4. Zakres rozszerzony. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 4.4., strona 25, Świat fizyki. Klasa 7. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 4, strona 72, Fizyka. Klasa 7. Podręcznik - rozwiązania i odpowiedzi

22

22

Ćwiczenie 1.3

22

22

22

22

23

22

23

23

23

24

Ćwiczenie 1.10

24

Ćwiczenie 1.11

22

24

24

24

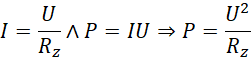
Ćwiczenie 2.4

25

25

25

25

25

25

25

26

Ćwiczenie 2.8

26

26

26

27

Ćwiczenie 3.1

27

27

27

27

27

27

27

Ćwiczenie 3.2

28

28

28

28

28

28

28

Ćwiczenie 3.7

29

29

29

Ćwiczenie 3.8

29

29

29

29

29

29

Ćwiczenie 3.10

29

Ćwiczenie 3.11

29

29

29

Ćwiczenie 3.12

30

30

30

Ćwiczenie 3.13

30

30

30

30

Ćwiczenie 3.14

30

30

30

Ćwiczenie 3.15

31

31

31

31

Ćwiczenie 3.16

31

31

31

31

Ćwiczenie 3.17

32

32

32

Ćwiczenie 3.18

32

Ćwiczenie 3.19

33

33

33

Ćwiczenie 3.20

33

33

33

33

Ćwiczenie 3.21

33

33

33

33

33

Ćwiczenie 3.22

33

34

34

34

35

35

35

35

35

35

Ćwiczenie 4.10

35

35

36

36

36

36

36

Ćwiczenie 5.7

36

36

36

36

Ćwiczenie 5.8

37

37

37

Ćwiczenie 5.9

37

37

37

Ćwiczenie 5.10

37

37

37

Ćwiczenie 5.11

37

Ćwiczenie 5.12

37

37

37

Ćwiczenie 5.13

38

38

38

38

38

38

38

39

39

Ćwiczenie 6.7

39

39

39

39

39

40

Ćwiczenie 6.10

40

40

40

40

Ćwiczenie 6.11

40

Ćwiczenie 6.12

40

40

40

40

41

41

Ćwiczenie 7.4

42

42

42

42

Ćwiczenie 7.5

42

42

42

42

42

Ćwiczenie 7.6

42

42

42

43

43

43

43

44

Ćwiczenie 8.4

44

44

44

Ćwiczenie 8.5

44

44

44

44

Ćwiczenie 8.6

45

45

45

45

Ćwiczenie 8.7

45

45

45

Ćwiczenie 8.8

45

45

45

45

Ćwiczenie 9.1

45

45

45

45

Ćwiczenie 9.3

46

46

46

46

Ćwiczenie 9.4

46

46

47

47

Ćwiczenie 9.5

47

47

47

Ćwiczenie 9.6

47

47

47

47

47

Ćwiczenie 9.7

48

48

48

48

Ćwiczenie 9.8

48

48

48

Ćwiczenie 9.9

48

48

48

Ćwiczenie 10.1

49

Ćwiczenie 10.2

49

49

49

49

Ćwiczenie 10.3

49

Ćwiczenie 10.4

49

49

49

49

49

Ćwiczenie 10.5

50

Ćwiczenie 10.6

50

50

50

50

Ćwiczenie 10.7

50

Ćwiczenie 10.8

50

Ćwiczenie 10.9

51

Ćwiczenie 11.1

51

Ćwiczenie 11.2

51

Ćwiczenie 11.3

52

52

52

52

Ćwiczenie 11.4

52

52

52

Ćwiczenie 11.5

52

52

52

Ćwiczenie 11.6

53

Ćwiczenie 11.7

53

Ćwiczenie 11.8

53

Ćwiczenie 11.9

54

Ćwiczenie 12.1

54

Ćwiczenie 12.2

54

54

54

54

Ćwiczenie 12.3

55

Ćwiczenie 12.4

55

55

55

Pełny spis treści