Zbiór zadań, Wydawnictwo: OE Pazdro

Zadanie 1.79, f) - strona 23

W tym zadaniu podaj wzór oraz dziedzinę funkcji g, której wykres powstał w wyniku przekształcenia wykresu funkcji f przez symetrię osiową względem osi OY. $\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

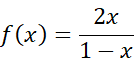
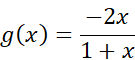
Aby obliczyć wzór funkcji g, której wykres jest symetryczny względem osi OY do wykresu funkcji f, zastosuj wzór $\text{[math]}$ . Aby znaleźć dziedzinę funkcji g, pamiętaj, że mianownik nie może mieć wartości równej 0.

Ćwiczenie A, strona 51, Matematyka z plusem. Klasa 8. Podręcznik – rozwiązania i odpowiedzi

Ćwiczenie 3., strona 170, Matematyka wokół nas. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Zadanie 9., strona 24, Matematyka 4. Klasa 4. Zbiór zadań. Zakres rozszerzony - rozwiązania i odpowiedzi

Zadanie 1., strona 179, Matematyka. Klasa 1. Podręcznik. Zakres rozszerzony. Część 2 – rozwiązania i odpowiedzi

Zadanie 10, strona 30, Matematyka wokół nas. Klasa 5. Zeszyt ćwiczeń. Część 1 – rozwiązania i odpowiedzi

Ćwiczenie sprawdzające 5, strona 40, Matematyka. Klasa 8. Podręcznik - rozwiązania i odpowiedzi

Ćwiczenie 6, strona 51, Matematyka. Klasa 8. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Zadanie 12., strona 56, Matematyka. Klasa 7. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 3, strona 149, Matematyka z plusem. Klasa 2. Podręcznik. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 29., strona 141, Matematyka. Klasa 7. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 1.1

7

7

7

7

7

7

7

7

7

7

Zadanie 1.3

7

7

7

7

7

7

Zadanie 1.5

8

8

8

8

8

Zadanie 1.6

8

8

8

8

8

Zadanie 1.7

8

8

8

8

8

Zadanie 1.8

8

8

8

8

8

8

Zadanie 1.10

8

8

8

Zadanie 1.11

8

8

8

8

8

Zadanie 1.12

9

9

9

9

9

Zadanie 1.13

9

9

9

9

Zadanie 1.15

9

9

9

9

9

Zadanie 1.17

9

9

9

Zadanie 1.18

9

9

9

Zadanie 1.19

9

9

9

9

10

10

Zadanie 1.22

10

10

10

10

Zadanie 1.23

10

10

10

10

Zadanie 1.24

10

10

10

Zadanie 1.25

10

10

10

Zadanie 1.26

10

10

10

10

10

11

11

Zadanie 1.29

11

11

11

Zadanie 1.30

11

11

11

11

11

11

11

Zadanie 1.31

12

12

12

12

12

12

12

Zadanie 1.32

12

12

12

Zadanie 1.33

12

12

12

Zadanie 1.34

12

12

12

12

Zadanie 1.35

12

12

12

12

Zadanie 1.36

12

12

12

Zadanie 1.37

13

13

13

13

13

13

Zadanie 1.39

13

13

13

13

Zadanie 1.40

13

13

13

13

13

Zadanie 1.41

13

13

13

13

13

Zadanie 1.42

14

14

14

Zadanie 1.43

14

14

14

Zadanie 1.44

14

14

14

15

15

Zadanie 1.45

15

15

15

15

15

15

15

16

Zadanie 1.49

16

16

16

16

16

16

16

Zadanie 1.50

16

16

16

16

16

Zadanie 1.51

16

16

16

16

Zadanie 1.52

17

17

17

17

Zadanie 1.53

17

17

17

17

Zadanie 1.54

17

17

17

17

Zadanie 1.55

17

17

17

Zadanie 1.56

17

17

17

17

17

Zadanie 1.57

17

17

17

17

Zadanie 1.58

18

18

18

18

Zadanie 1.59

18

18

18

18

Zadanie 1.61

18

18

18

18

18

Zadanie 1.62

18

18

18

18

18

18

18

Zadanie 1.63

19

19

19

19

19

Zadanie 1.64

19

19

19

19

19

19

19

Zadanie 1.65

19

19

19

19

19

19

19

Zadanie 1.66

19

19

19

19

Zadanie 1.67

20

20

20

20

20

Zadanie 1.68

20

20

20

20

20

Zadanie 1.69

20

20

20

20

20

Zadanie 1.70

21

21

21

21

21

Zadanie 1.71

21

21

21

Zadanie 1.72

21

21

21

21

21

Zadanie 1.73

22

22

22

22

22

22

22

Zadanie 1.74

22

22

22

22

22

22

22

Zadanie 1.75

22

22

22

Zadanie 1.76

22

22

22

Zadanie 1.77

23

23

23

23

23

Zadanie 1.78

23

23

23

23

23

23

23

Zadanie 1.79

23

23

23

23

23

23

23

Zadanie 1.80

23

23

23

Zadanie 1.81

24

24

24

24

24

24

24

Zadanie 1.82

24

24

24

24

24

Zadanie 1.83

24

24

24

24

Zadanie 1.84

24

24

24

Zadanie 1.85

24

24

24

Zadanie 1.86

25

25

25

25

25

Zadanie 1.87

25

25

25

25

Zadanie 1.88

26

26

26

Zadanie 1.89

26

26

26

26

26

Zadanie 1.90

26

26

26

26

26

26

26

Zadanie 1.91

27

27

27

27

27

Zadanie 1.92

27

27

27

27

27

Zadanie 1.93

27

27

27

27

27

27

27

27

27

27

Zadanie 1.97

27

27

27

27

Zadanie 1.98

28

28

28

28

Zadanie 1.99

28

28

28

28

28

28

28

Zadanie 1.103

28

28

28

Zadanie 1.104

28

28

28

28

Zadanie 1.105

28

28

28

28

28

28

29

29

29

29

29

29

30

30

31

31

31

31

31

Zadanie 16

31

31

31

31

31

32

Zadanie 20

32

32

32

Zadanie 21

32

32

32

32

Zadanie 23

32

32

32

32

Zadanie 24

32

32

32

Zadanie 25

32

32

32

Zadanie 26

33

33

33

Zadanie 27

33

33

33

33

Zadanie 28

33

33

33

Zadanie 29

33

33

33

33

Zadanie 30

33

33

33

33

Zadanie 31

33

33

33

33

Zadanie 32

33

33

33

33

33

Pełny spis treści