Zbiór zadań, Wydawnictwo: OE Pazdro

Zadanie 19 - strona 32

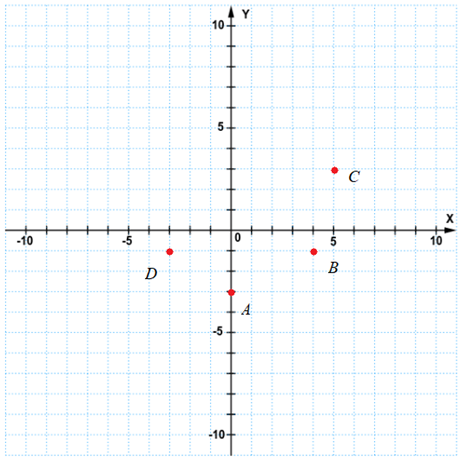
Dane są punkty $\text{[math]}$ W tym zadaniu musisz udowodnić, że czworokąt ABCD jest trapezem.

Założenia:

$\text{[math]}$

Teza:

Czworokąt ABCD jest trapezem.

Dowód:

Obliczamy współrzędne wektorów tworzących boki:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Szukamy pary równoległych wektorów:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

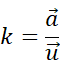
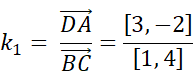
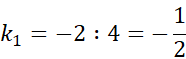
Sprzeczność

$\text{[math]}$

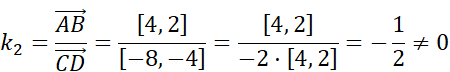
figura ABCD ma parę równoległych boków, czyli czworokąt ABCD jest trapezem

c. n. d.

Aby dowieść, że czworokąt ABCD jest trapezem, musimy pokazać, że ma przynajmniej jedną parę równoległych boków. Wektory niezerowe u, a są równoległe wtedy i tylko wtedy, gdy istnieje liczba $\text{[math]}$ taka, że $\text{[math]}$ Wektory $\text{[math]}$ i $\text{[math]}$ są równoległe, z czego wynika, że czworokąt ABCD jest trapezem.

Zadanie 14, strona 111, Teraz matura. Klasa 4. Zbiór zadań. Poziom podstawowy – rozwiązania i odpowiedzi

Zadanie 8., strona 45, Matematyka z kluczem. Klasa 8. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 1.8., strona 119, Prosto do matury. Klasa 4. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Ćwiczenie 8., strona 53, Matematyka wokół nas. Klasa 5. Podręcznik - rozwiązania i odpowiedzi

Zadanie 4, strona 114, Matematyka z kluczem. Klasa 6. Podręcznik. Część 1 – rozwiązania i odpowiedzi

Zadanie 4, strona 130, Matematyka. Klasa 6. Podręcznik - rozwiązania i odpowiedzi

Zadanie 8.126., strona 211, Matematyka. Klasa 3. Zbiór zadań. Zakres rozszerzony – rozwiązania i odpowiedzi

Zadanie 22, strona 150, Matematyka z plusem. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie 5, strona 78, Matematyka z plusem. Klasa 2. Ćwiczenia podstawowe – rozwiązania i odpowiedzi

Zadanie 6., strona 422, Matematyka. Klasa 1. Podręcznik. Zakres podstawowy - rozwiązania i odpowiedzi

Zadanie 1.1

7

7

7

7

7

7

7

7

7

7

Zadanie 1.3

7

7

7

7

7

7

Zadanie 1.5

8

8

8

8

8

Zadanie 1.6

8

8

8

8

8

Zadanie 1.7

8

8

8

8

8

Zadanie 1.8

8

8

8

8

8

8

Zadanie 1.10

8

8

8

Zadanie 1.11

8

8

8

8

8

Zadanie 1.12

9

9

9

9

9

Zadanie 1.13

9

9

9

9

Zadanie 1.15

9

9

9

9

9

Zadanie 1.17

9

9

9

Zadanie 1.18

9

9

9

Zadanie 1.19

9

9

9

9

10

10

Zadanie 1.22

10

10

10

10

Zadanie 1.23

10

10

10

10

Zadanie 1.24

10

10

10

Zadanie 1.25

10

10

10

Zadanie 1.26

10

10

10

10

10

11

11

Zadanie 1.29

11

11

11

Zadanie 1.30

11

11

11

11

11

11

11

Zadanie 1.31

12

12

12

12

12

12

12

Zadanie 1.32

12

12

12

Zadanie 1.33

12

12

12

Zadanie 1.34

12

12

12

12

Zadanie 1.35

12

12

12

12

Zadanie 1.36

12

12

12

Zadanie 1.37

13

13

13

13

13

13

Zadanie 1.39

13

13

13

13

Zadanie 1.40

13

13

13

13

13

Zadanie 1.41

13

13

13

13

13

Zadanie 1.42

14

14

14

Zadanie 1.43

14

14

14

Zadanie 1.44

14

14

14

15

15

Zadanie 1.45

15

15

15

15

15

15

15

16

Zadanie 1.49

16

16

16

16

16

16

16

Zadanie 1.50

16

16

16

16

16

Zadanie 1.51

16

16

16

16

Zadanie 1.52

17

17

17

17

Zadanie 1.53

17

17

17

17

Zadanie 1.54

17

17

17

17

Zadanie 1.55

17

17

17

Zadanie 1.56

17

17

17

17

17

Zadanie 1.57

17

17

17

17

Zadanie 1.58

18

18

18

18

Zadanie 1.59

18

18

18

18

Zadanie 1.61

18

18

18

18

18

Zadanie 1.62

18

18

18

18

18

18

18

Zadanie 1.63

19

19

19

19

19

Zadanie 1.64

19

19

19

19

19

19

19

Zadanie 1.65

19

19

19

19

19

19

19

Zadanie 1.66

19

19

19

19

Zadanie 1.67

20

20

20

20

20

Zadanie 1.68

20

20

20

20

20

Zadanie 1.69

20

20

20

20

20

Zadanie 1.70

21

21

21

21

21

Zadanie 1.71

21

21

21

Zadanie 1.72

21

21

21

21

21

Zadanie 1.73

22

22

22

22

22

22

22

Zadanie 1.74

22

22

22

22

22

22

22

Zadanie 1.75

22

22

22

Zadanie 1.76

22

22

22

Zadanie 1.77

23

23

23

23

23

Zadanie 1.78

23

23

23

23

23

23

23

Zadanie 1.79

23

23

23

23

23

23

23

Zadanie 1.80

23

23

23

Zadanie 1.81

24

24

24

24

24

24

24

Zadanie 1.82

24

24

24

24

24

Zadanie 1.83

24

24

24

24

Zadanie 1.84

24

24

24

Zadanie 1.85

24

24

24

Zadanie 1.86

25

25

25

25

25

Zadanie 1.87

25

25

25

25

Zadanie 1.88

26

26

26

Zadanie 1.89

26

26

26

26

26

Zadanie 1.90

26

26

26

26

26

26

26

Zadanie 1.91

27

27

27

27

27

Zadanie 1.92

27

27

27

27

27

Zadanie 1.93

27

27

27

27

27

27

27

27

27

27

Zadanie 1.97

27

27

27

27

Zadanie 1.98

28

28

28

28

Zadanie 1.99

28

28

28

28

28

28

28

Zadanie 1.103

28

28

28

Zadanie 1.104

28

28

28

28

Zadanie 1.105

28

28

28

28

28

28

29

29

29

29

29

29

30

30

31

31

31

31

31

Zadanie 16

31

31

31

31

31

32

Zadanie 20

32

32

32

Zadanie 21

32

32

32

32

Zadanie 23

32

32

32

32

Zadanie 24

32

32

32

Zadanie 25

32

32

32

Zadanie 26

33

33

33

Zadanie 27

33

33

33

33

Zadanie 28

33

33

33

Zadanie 29

33

33

33

33

Zadanie 30

33

33

33

33

Zadanie 31

33

33

33

33

Zadanie 32

33

33

33

33

33

Pełny spis treści