Zapoznaj się z poniższą definicją, a następnie wykonaj ćwiczenia.
„Prostą k nazywamy osią symetrii figury F wtedy, gdy obrazem figury F w symetrii względem prostej k jest ta sama figura F, czyli
![]() Figury, które mają oś symetrii, nazywamy figurami osiowosymetrycznymi”.
Figury, które mają oś symetrii, nazywamy figurami osiowosymetrycznymi”.
W tym zadaniu musisz podać, ile osi symetrii mają trójkąty: różnoboczny, równoramienny i równoboczny.
- różnoboczny — zero
- równoramienny, który nie jest równoboczny — jedna
- równoboczny — trzy

Na rysunku zaznaczono osie symetrii. Trójkąt różnoboczny nie ma osi symetrii, trójkąt równoramienny ma jedną, a równoboczny ma trzy osie symetrii.
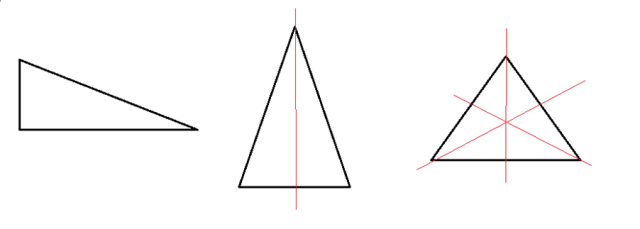

Zadanie 1.1
7Zadanie 1.3
7Zadanie 1.5
8Zadanie 1.6
8Zadanie 1.7
8Zadanie 1.8
8Zadanie 1.10
8Zadanie 1.11
8Zadanie 1.12
9Zadanie 1.13
9Zadanie 1.15
9Zadanie 1.17
9Zadanie 1.18
9Zadanie 1.19
9Zadanie 1.22
10Zadanie 1.23
10Zadanie 1.24
10Zadanie 1.25
10Zadanie 1.26
10Zadanie 1.29
11Zadanie 1.30
11Zadanie 1.31
12Zadanie 1.32
12Zadanie 1.33
12Zadanie 1.34
12Zadanie 1.35
12Zadanie 1.36
12Zadanie 1.37
13Zadanie 1.39
13Zadanie 1.40
13Zadanie 1.41
13Zadanie 1.42
14Zadanie 1.43
14Zadanie 1.44
14Zadanie 1.45
15Zadanie 1.49
16Zadanie 1.50
16Zadanie 1.51
16Zadanie 1.52
17Zadanie 1.53
17Zadanie 1.54
17Zadanie 1.55
17Zadanie 1.56
17Zadanie 1.57
17Zadanie 1.58
18Zadanie 1.59
18Zadanie 1.61
18Zadanie 1.62
18Zadanie 1.63
19Zadanie 1.64
19Zadanie 1.65
19Zadanie 1.66
19Zadanie 1.67
20Zadanie 1.68
20Zadanie 1.69
20Zadanie 1.70
21Zadanie 1.71
21Zadanie 1.72
21Zadanie 1.73
22Zadanie 1.74
22Zadanie 1.75
22Zadanie 1.76
22Zadanie 1.77
23Zadanie 1.78
23Zadanie 1.79
23Zadanie 1.80
23Zadanie 1.81
24Zadanie 1.82
24Zadanie 1.83
24Zadanie 1.84
24Zadanie 1.85
24Zadanie 1.86
25Zadanie 1.87
25Zadanie 1.88
26Zadanie 1.89
26Zadanie 1.90
26Zadanie 1.91
27Zadanie 1.92
27Zadanie 1.93
27Zadanie 1.97
27Zadanie 1.98
28Zadanie 1.99
28Zadanie 1.103
28Zadanie 1.104
28Zadanie 1.105
28Zadanie 16
31Zadanie 20
32Zadanie 21
32Zadanie 23
32Zadanie 24
32Zadanie 25
32Zadanie 26
33Zadanie 27
33Zadanie 28
33Zadanie 29
33Zadanie 30
33Zadanie 31
33Zadanie 32
33
