A = (-8, 0), B = (0, 6). Narysuj odcinki symetryczne do tych punktów: jeden względem osi y oraz drugi względem osi x. Skonstruuj także trzeci odcinek symetryczny względem osi y do drugiego narysowanego przez ciebie odcinka. Oblicz pole AB₁A₂B3. Gdzie jest środek symetrii tej figury?
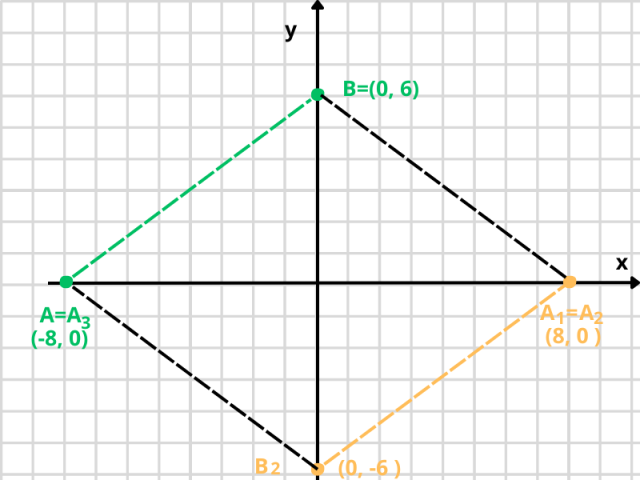
Przekątne powstałego rombu:
|AA1| = 8 + 8 = 16
|BB2| = 6 + 6 = 12
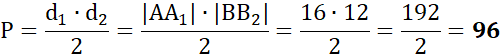
|AB2| obliczymy z Twierdzenia Pitagorasa:
62 + 82 = |AB2|2
36 + 64 = |AB2|2
|AB2|2 = 100
|AB2| = 10
Obw. = 4 · 10 = 40
Odp.: Jest to romb o środku symetrii w punkcie (0, 0). Jego pole wynosi 96, a obwód 40.

Jeżeli dana figura i figura do niej symetryczna pokrywają się, to wówczas punkt S jest środkiem symetrii.

Zadanie 1.
270Zadanie 3.
270Zadanie 7.
278Zadanie 12.
280Zadanie 18.
280Zadanie 2.
284Zadanie 4.
284Zadanie 6.
284Zadanie 8.
284Zadanie 11.
285Zadanie 12.
285Zadanie Sprawdź się! 2.
286Zadanie 1.
288Zadanie 12.
290Zadanie 2.
293Zadanie 4.
293Zadanie 5.
293Zadanie 6.
294Zadanie 8.
294Zadanie Wyzwanie 1.
295Zadanie Sprawdź się! 3.
295Ćwiczenie 5.
296Ćwiczenie 6.
297
