Trapez ABCD jest symetryczny do ABC1D1 względem prostej, która zawiera podstawę AB. |AB| = 6 cm, |CD| = 3 cm, |AD| = 4 cm. Kąt ABC jest ostry. Oblicz pole DD₁C₁BC.
A. 18 cm²
B. 36 cm²
Oblicz obwód DD₁C₁BC.
C. 24 cm
D. 30 cm
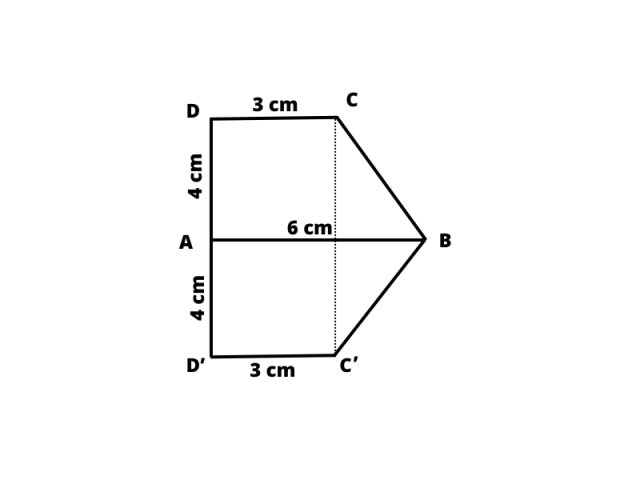
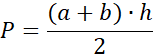
Zauważ, że pole DD₁C₁BC to pole dwóch trapezów, więc:
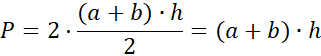
P = (6 + 3) · 4 = 36 cm2
Odp.: B. 36 cm2
32 + 42 = |C’B|2
9 + 16 = |C’B|2
![]()
|C’B| = 5 cm
|CB| = 5 cm
Obw. = 8 cm + 6 cm + 10 cm = 24 cm
C. 24 cm

Pamiętaj, że dwa różne punkty są symetryczne względem jakiejś prostej gdy ta prosta jest symetralna odcinka jaki tworzą te punkty.

Zadanie 1.
270Zadanie 3.
270Zadanie 7.
278Zadanie 12.
280Zadanie 18.
280Zadanie 2.
284Zadanie 4.
284Zadanie 6.
284Zadanie 8.
284Zadanie 11.
285Zadanie 12.
285Zadanie Sprawdź się! 2.
286Zadanie 1.
288Zadanie 12.
290Zadanie 2.
293Zadanie 4.
293Zadanie 5.
293Zadanie 6.
294Zadanie 8.
294Zadanie Wyzwanie 1.
295Zadanie Sprawdź się! 3.
295Ćwiczenie 5.
296Ćwiczenie 6.
297
