Zadanie
Sporządź rysunek kąta o mierze 60° i wierzchołku S, a następnie zaznacz w jego pobliży dowolny punkt P. Odszukaj punkty symetryczne do punktu P względem ramion kąta i podaj miar kąta ASB.
Rozwiązanie
Kąt ABP to różnica między 360° (ilość stopni w każdym czworokącie) a sumą pozostałych kątów w tym czworokącie:
360° - 60° - 90° - 90° =120°
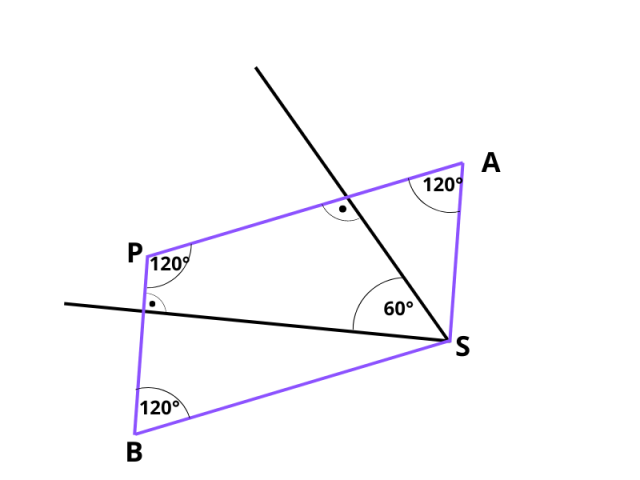
Zauważ, że APBS to równoległobok, a z jego własności wiemy, że kąty leżące naprzeciw siebie mają taką samą miarę. W związku z tym, skoro kąt APB ma miarę 120°, kąt ASB również ma miarę 120°.
Wyjaśnienie
Pamiętaj, że figury symetryczne są przystające. Szukając punktów symetrycznych do punktu P względem ramion kąta musisz poprowadzić prostopadłe odcinki do ramion kąta i przenieść odległość na drugą stronę prostej.
Matematyka - wybrane pytania
REKLAMA
Zadania z tego działu
Symetrie
268
1. Symetralna odcinka i dwusieczna kąta
268
Zadanie 1.
270Zadanie 3.
270
2. Symetria osiowa
275
Zadanie 7.
278Zadanie 12.
280Zadanie 18.
280
3. Figury osiowosymetryczne
282
Zadanie 2.
284Zadanie 4.
284Zadanie 6.
284Zadanie 8.
284Zadanie 11.
285Zadanie 12.
285Zadanie Sprawdź się! 2.
286
4. Symetria środkowa
287
Zadanie 1.
288Zadanie 12.
290
5. Figury środkowosymetryczne
292
Zadanie 2.
293Zadanie 4.
293Zadanie 5.
293Zadanie 6.
294Zadanie 8.
294Zadanie Wyzwanie 1.
295Zadanie Sprawdź się! 3.
295
Zadania utrwalające
296
Ćwiczenie 5.
296Ćwiczenie 6.
297
Zadania sprawdzające
298