Podaj pole czworokąta K₁K₂K3K4, jeśli punkty będące wierzchołkami są punktami symetrycznymi do punktu K względem prostych zawierających boki prostokąta ABCD o wymiarach 5 cm x 3 cm. Punkt K zaznaczono wewnątrz prostokąta.
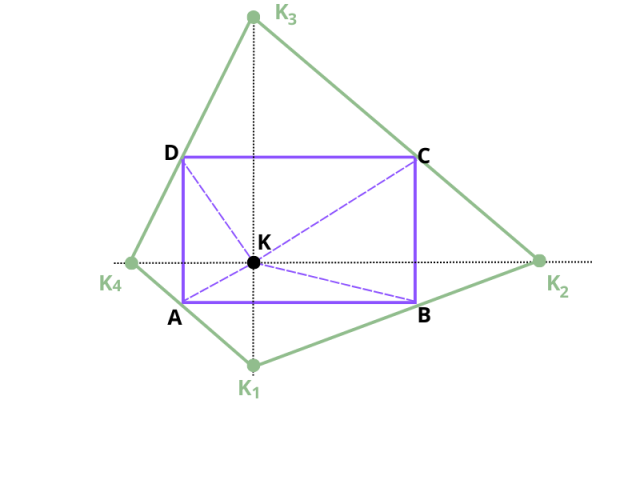
PK1K2K3K4 = 2 PABCD
PABCD = 3 cm · 5 cm = 15 cm2
Pcz = 2 · 15 cm2 = 30 cm2
Odp.: Pole tego czworokąta wynosi 30 cm2.

Zauważ, że trójkąty DCK3 i DKC, CBK2 i DBK, ABK1 i ABK oraz ADK4 i ADK są przystające i suma ich pól jest równa polu prostokąta. Prostokąt ABCD jest więc złożony z czterech trójkątów, a czworokąt K₁K₂K3K4 jest złożony z ośmiu trójkątów, z których każdy ma parę przystającą.

Zadanie 1.
270Zadanie 3.
270Zadanie 7.
278Zadanie 12.
280Zadanie 18.
280Zadanie 2.
284Zadanie 4.
284Zadanie 6.
284Zadanie 8.
284Zadanie 11.
285Zadanie 12.
285Zadanie Sprawdź się! 2.
286Zadanie 1.
288Zadanie 12.
290Zadanie 2.
293Zadanie 4.
293Zadanie 5.
293Zadanie 6.
294Zadanie 8.
294Zadanie Wyzwanie 1.
295Zadanie Sprawdź się! 3.
295Ćwiczenie 5.
296Ćwiczenie 6.
297
