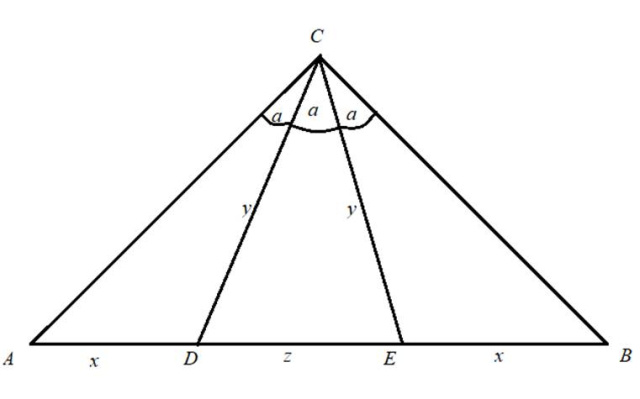
W trójkącie prostokątnym równoramiennym ABC przyprostokątne mają długość: |AC| = |BC| = √2. Punkty D, E należą do przeciwprostokątnej AB oraz | ∢ACD| = | ∢ DCE| = | ∢ ECB|. W tym zadaniu musisz obliczyć długości odcinków AD, DE, EB.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
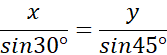
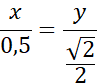
![]()
![]()
![]()
w trójkącie ADC z tw. cosinusów:
![]()
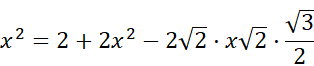
![]()
![]()
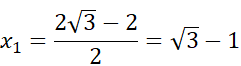
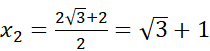 – nie może być, bo jest większe od |AB|
– nie może być, bo jest większe od |AB|
Odp.:
![]()

Wykorzystaj twierdzenie sinusów: w dowolnym trójkącie stosunek długości dowolnego boku do sinusa kąta naprzeciw tego boku jest stały i równy długości średnicy okręgu opisanego na trójkącie.
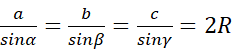 , R – to długość promienia okręgu opisanego na trójkącie. Wykorzystaj twierdzenie cosinusów: w dowolnym trójkącie kwadrat długości jednego boku jest równy sumie kwadratów długości dwóch pozostałych boków, zmniejszonej o podwojony iloczyn długości tych boków i cosinusa kąta zawartego między nimi.
, R – to długość promienia okręgu opisanego na trójkącie. Wykorzystaj twierdzenie cosinusów: w dowolnym trójkącie kwadrat długości jednego boku jest równy sumie kwadratów długości dwóch pozostałych boków, zmniejszonej o podwojony iloczyn długości tych boków i cosinusa kąta zawartego między nimi.

Zadanie 7.1
128Zadanie 7.2
128Zadanie 7.3
128Zadanie 7.4
128Zadanie 7.5
128Zadanie 7.6
129Zadanie 7.9
129Zadanie 7.10
129Zadanie 7.12
129Zadanie 7.14
130Zadanie 7.17
130Zadanie 7.19
130Zadanie 7.24
131Zadanie 7.27
131Zadanie 7.28
131Zadanie 7.30
131Zadanie 7.36
132Zadanie 7.37
133Zadanie 7.39
134Zadanie 7.46
134Zadanie 7.47
134Zadanie 7.50
135Zadanie 7.52
135Zadanie 7.53
135Zadanie 7.54
135Zadanie 7.60
136Zadanie 7.62
136Zadanie 7.68
137Zadanie 7.69
137Zadanie 7.70
137Zadanie 7.73
137Zadanie 7.74
138Zadanie 7.75
138Zadanie 7.77
138Zadanie 7.78
138Zadanie 7.79
138Zadanie 7.80
138Zadanie 7.81
139Zadanie 7.82
139Zadanie 7.85
139Zadanie 7.86
139Zadanie 7.87
139Zadanie 7.88
140Zadanie 7.91
140Zadanie 7.92
140Zadanie 7.97
141Zadanie 7.105
142Zadanie 7.106
143Zadanie 7.108
143Zadanie 7.109
143Zadanie 7.110
143Zadanie 7.114
144Zadanie 7.124
145Zadanie 7.125
145Zadanie 17
148Zadanie 19
148Zadanie 22
149Zadanie 23
149Zadanie 24
149Zadanie 25
149Zadanie 26
149Zadanie 33
150Zadanie 34
150
