Na boku AC trójkąta ABC zaznaczono punkty D, E w taki sposób, że |AE| = |ED| = |DC|. Przez punkty E, D poprowadzono proste równoległe do boku AB, które podzieliły trójkąt na trzy rozłączne figury o polach równych odpowiednio P1, P2, P3. W tym zadaniu musisz określić stosunek pola P2 do P3.
A. P2 : P3 = 1 : 2
B. P2 : P3 = 2 : 3
C. P2 : P3 = 4 : 9
D. P2 : P3 = 3 : 5
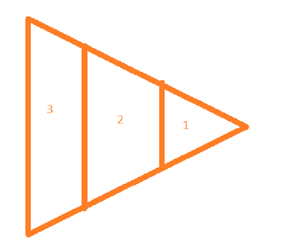
Trójkąt 1 jest podobny do trójkąta 3 w skali
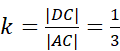
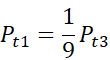
Trójkąt 2 jest podobny do trójkąta 3 w skali
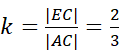
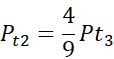
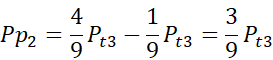
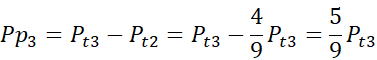
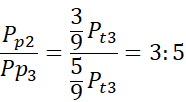
Odpowiedź D jest prawidłowa.

Oblicz skalę podobieństwa trójkątów podobnych, a następnie ich pola, z których obliczysz pola czworokątów.

Zadanie 7.1
128Zadanie 7.2
128Zadanie 7.3
128Zadanie 7.4
128Zadanie 7.5
128Zadanie 7.6
129Zadanie 7.9
129Zadanie 7.10
129Zadanie 7.12
129Zadanie 7.14
130Zadanie 7.17
130Zadanie 7.19
130Zadanie 7.24
131Zadanie 7.27
131Zadanie 7.28
131Zadanie 7.30
131Zadanie 7.36
132Zadanie 7.37
133Zadanie 7.39
134Zadanie 7.46
134Zadanie 7.47
134Zadanie 7.50
135Zadanie 7.52
135Zadanie 7.53
135Zadanie 7.54
135Zadanie 7.60
136Zadanie 7.62
136Zadanie 7.68
137Zadanie 7.69
137Zadanie 7.70
137Zadanie 7.73
137Zadanie 7.74
138Zadanie 7.75
138Zadanie 7.77
138Zadanie 7.78
138Zadanie 7.79
138Zadanie 7.80
138Zadanie 7.81
139Zadanie 7.82
139Zadanie 7.85
139Zadanie 7.86
139Zadanie 7.87
139Zadanie 7.88
140Zadanie 7.91
140Zadanie 7.92
140Zadanie 7.97
141Zadanie 7.105
142Zadanie 7.106
143Zadanie 7.108
143Zadanie 7.109
143Zadanie 7.110
143Zadanie 7.114
144Zadanie 7.124
145Zadanie 7.125
145Zadanie 17
148Zadanie 19
148Zadanie 22
149Zadanie 23
149Zadanie 24
149Zadanie 25
149Zadanie 26
149Zadanie 33
150Zadanie 34
150
