W kole z jednego punktu okręgu poprowadzono dwie cięciwy; każda ma długość 6 cm. Utworzyły one kąt 60°.W tym zadaniu musisz obliczyć pole części koła zawartej między tymi cięciwami.
Trójkąt 1 utworzony przez cięciwy jest równoboczny x= 6

Trójkąt 2 utworzony z promieni okręgu oparty na tym samym łuku co trójkąt 1, posiada tę samą podstawę co trójkąt 1 , x=6
![]()
![]() = 2R
= 2R
2R=6
![]()
2R=
![]()
![]() cm
cm
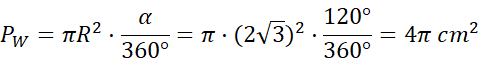
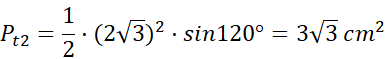
![]()

Zauważ, że trójkąt ABC jest równoboczny, a następnie oblicz jego pole. Oblicz R ze wzoru na pole trójkąta
![]() . Następnie oblicz pole wycinka koła ze wzoru
. Następnie oblicz pole wycinka koła ze wzoru
![]() i pole trójkąta BOC ze wzoru:
i pole trójkąta BOC ze wzoru:
![]() .
.

Zadanie 7.1
128Zadanie 7.2
128Zadanie 7.3
128Zadanie 7.4
128Zadanie 7.5
128Zadanie 7.6
129Zadanie 7.9
129Zadanie 7.10
129Zadanie 7.12
129Zadanie 7.14
130Zadanie 7.17
130Zadanie 7.19
130Zadanie 7.24
131Zadanie 7.27
131Zadanie 7.28
131Zadanie 7.30
131Zadanie 7.36
132Zadanie 7.37
133Zadanie 7.39
134Zadanie 7.46
134Zadanie 7.47
134Zadanie 7.50
135Zadanie 7.52
135Zadanie 7.53
135Zadanie 7.54
135Zadanie 7.60
136Zadanie 7.62
136Zadanie 7.68
137Zadanie 7.69
137Zadanie 7.70
137Zadanie 7.73
137Zadanie 7.74
138Zadanie 7.75
138Zadanie 7.77
138Zadanie 7.78
138Zadanie 7.79
138Zadanie 7.80
138Zadanie 7.81
139Zadanie 7.82
139Zadanie 7.85
139Zadanie 7.86
139Zadanie 7.87
139Zadanie 7.88
140Zadanie 7.91
140Zadanie 7.92
140Zadanie 7.97
141Zadanie 7.105
142Zadanie 7.106
143Zadanie 7.108
143Zadanie 7.109
143Zadanie 7.110
143Zadanie 7.114
144Zadanie 7.124
145Zadanie 7.125
145Zadanie 17
148Zadanie 19
148Zadanie 22
149Zadanie 23
149Zadanie 24
149Zadanie 25
149Zadanie 26
149Zadanie 33
150Zadanie 34
150
