W trójkącie ABC boki mają długość: |AB| = 10 cm, |BC| = 2√21 cm i |AC| = 8 cm. W tym zadaniu musisz obliczyć długości środkowych CD i BE.
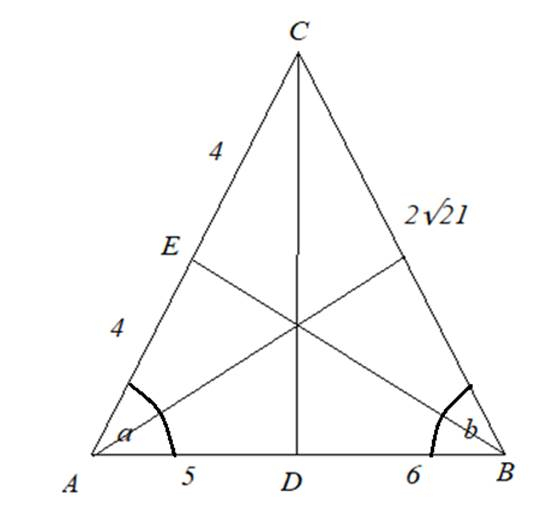
z trójkąta ABC:
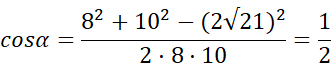
z trójkąta ADC:
![]()
![]()
![]()
![]() cm
cm
z trójkąta ABE:
![]()
![]()
![]() cm
cm

Środkowe trójkąta przecinają się w jednym punkcie, zwanym środkiem ciężkości trójkąta. Środek ciężkości dzieli każdą ze środkowych w stosunku 2:1, przy czym dłuższy jest odcinek łączący środek ciężkości z wierzchołkiem trójkąta. Twierdzenie cosinusów: w dowolnym trójkącie kwadrat długości jednego boku jest równy sumie kwadratów długości dwóch pozostałych boków, zmniejszonej o podwojony iloczyn długości tych boków i cosinusa kąta zawartego między nimi.

Zadanie 7.1
128Zadanie 7.2
128Zadanie 7.3
128Zadanie 7.4
128Zadanie 7.5
128Zadanie 7.6
129Zadanie 7.9
129Zadanie 7.10
129Zadanie 7.12
129Zadanie 7.14
130Zadanie 7.17
130Zadanie 7.19
130Zadanie 7.24
131Zadanie 7.27
131Zadanie 7.28
131Zadanie 7.30
131Zadanie 7.36
132Zadanie 7.37
133Zadanie 7.39
134Zadanie 7.46
134Zadanie 7.47
134Zadanie 7.50
135Zadanie 7.52
135Zadanie 7.53
135Zadanie 7.54
135Zadanie 7.60
136Zadanie 7.62
136Zadanie 7.68
137Zadanie 7.69
137Zadanie 7.70
137Zadanie 7.73
137Zadanie 7.74
138Zadanie 7.75
138Zadanie 7.77
138Zadanie 7.78
138Zadanie 7.79
138Zadanie 7.80
138Zadanie 7.81
139Zadanie 7.82
139Zadanie 7.85
139Zadanie 7.86
139Zadanie 7.87
139Zadanie 7.88
140Zadanie 7.91
140Zadanie 7.92
140Zadanie 7.97
141Zadanie 7.105
142Zadanie 7.106
143Zadanie 7.108
143Zadanie 7.109
143Zadanie 7.110
143Zadanie 7.114
144Zadanie 7.124
145Zadanie 7.125
145Zadanie 17
148Zadanie 19
148Zadanie 22
149Zadanie 23
149Zadanie 24
149Zadanie 25
149Zadanie 26
149Zadanie 33
150Zadanie 34
150
