W trójkącie ostrokątnym równoramiennym ABC, |AC| = |BC|, poprowadzono wysokości CD i BE. Pole trójkąta ABE jest o 44% większe od pola trójkąta ADC. Wiedząc, że obwód trójkąta ABC jest równy 80 cm. W tym zadaniu musisz obliczyć pole trójkąta ABC.
Trójkąt ABE jest podobny do trójkąta ADC z cechy kkk
![]()
![]()
![]()
|AB|=1,2|AC|
|AC|=|BC|
![]() cm
cm
![]() =80:3,2=25cm
=80:3,2=25cm
|AB|=30cm
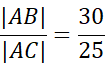
|DB|=30:2 = 15
![]()
![]()
![]() cm
cm
![]() cm²
cm²

Znajdź trójkąty podobne, a następnie oblicz ich skalę podobieństwa.
![]() stanowi skalę podobieństwa pól trójkątów podobnych. Na podstawie skali podobieństwa i obwodu znajdź długości boków trójkąta ABC. Oblicz wysokość z twierdzenia Pitagorasa, a następnie pole ze wzoru
stanowi skalę podobieństwa pól trójkątów podobnych. Na podstawie skali podobieństwa i obwodu znajdź długości boków trójkąta ABC. Oblicz wysokość z twierdzenia Pitagorasa, a następnie pole ze wzoru
![]()

Zadanie 7.1
128Zadanie 7.2
128Zadanie 7.3
128Zadanie 7.4
128Zadanie 7.5
128Zadanie 7.6
129Zadanie 7.9
129Zadanie 7.10
129Zadanie 7.12
129Zadanie 7.14
130Zadanie 7.17
130Zadanie 7.19
130Zadanie 7.24
131Zadanie 7.27
131Zadanie 7.28
131Zadanie 7.30
131Zadanie 7.36
132Zadanie 7.37
133Zadanie 7.39
134Zadanie 7.46
134Zadanie 7.47
134Zadanie 7.50
135Zadanie 7.52
135Zadanie 7.53
135Zadanie 7.54
135Zadanie 7.60
136Zadanie 7.62
136Zadanie 7.68
137Zadanie 7.69
137Zadanie 7.70
137Zadanie 7.73
137Zadanie 7.74
138Zadanie 7.75
138Zadanie 7.77
138Zadanie 7.78
138Zadanie 7.79
138Zadanie 7.80
138Zadanie 7.81
139Zadanie 7.82
139Zadanie 7.85
139Zadanie 7.86
139Zadanie 7.87
139Zadanie 7.88
140Zadanie 7.91
140Zadanie 7.92
140Zadanie 7.97
141Zadanie 7.105
142Zadanie 7.106
143Zadanie 7.108
143Zadanie 7.109
143Zadanie 7.110
143Zadanie 7.114
144Zadanie 7.124
145Zadanie 7.125
145Zadanie 17
148Zadanie 19
148Zadanie 22
149Zadanie 23
149Zadanie 24
149Zadanie 25
149Zadanie 26
149Zadanie 33
150Zadanie 34
150
