W tym zadaniu należy uzasadnić, że w zbiorze liczb rzeczywistych podane równanie nie ma rozwiązania.
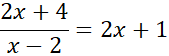
Określamy dziedzinę równania, pokazując, że mianownik ma być niezerowy. Mnożymy obydwie strony przez mianownik i doprowadzamy równanie do postaci trójmianu kwadratowego oraz liczymy jego wyróżnik. Okazuje się, że jest to liczba, która po spierwiastkowaniu jest liczbą nienależącą do zbioru liczb całkowitych, zatem żadne z rozwiązań nie będzie całkowite.