W tym zadaniu musisz obliczyć, na ile sposobów można utworzyć napis, w którym występuje co najmniej jedna samogłoska, wiedząc, że powstałe napisy są trzyliterowe oraz że pierwsza litera należy do zbioru ![]()
![]()
![]()
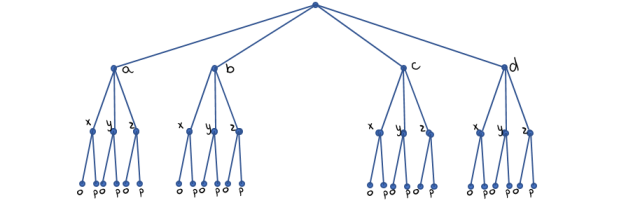
I sposób:
![]()
Możliwości ułożenia takiego napisu, gdzie jest co najmniej jedna samogłoska, jest dokładnie 18.
II sposób:
Obliczam, ile będzie napisów, gdzie nie pojawi się ani jedna samogłoska: (b, x, p), (b, z, p), (c, x, p), (c, z, p), (d, x, p), (d, z, p). Takich napisów jest 6.
A więc od wszystkich możliwości odejmiemy te, w których nie pojawi się żadna samogłoska:
![]()
Możliwości ułożenia takiego napisu, gdzie jest co najmniej jedna samogłoska, jest dokładnie 18.

W sposobie I odczytując z drzewa, zapisz ilość sposobów, na które można ułożyć taki napis, aby była co najmniej jedna samogłoska, wszystkie możliwości zsumuj. W II sposobie oblicz ile jest możliwości utworzenia napisów, tak aby nie pojawiła się w nich żadna samogłoska, następnie oblicz ilość wszystkich możliwości utworzenia napisu i oblicz różnicę.

Zadanie 4.
104Zadanie 5.
104Zadanie 8.
104Zadanie 9.
104Zadanie 10.
104Zadanie 11.
105Zadanie 12.
105Zadanie 13.
105Zadanie 14.
105Zadanie 15.
105Zadanie 16.
105Zadanie 4.
111Zadanie 5.
111Zadanie 6.
111Zadanie 7.
111Zadanie 8.
111Zadanie 9.
111Zadanie 10.
111Zadanie 2.
114Zadanie 3.
115Zadanie 5.
117Zadanie 6.
117Zadanie 7.
117Zadanie 8.
117Zadanie 9.
117Zadanie 11.
117Zadanie 13.
118Zadanie 14.
118Zadanie 15.
118Zadanie 16.
118Zadanie 17.
118Zadanie 1.
119Zadanie 4.
121Zadanie 6.
125Zadanie 7.
125Zadanie 8.
125Zadanie 10.
125Zadanie 14.
126Zadanie 15.
126Zadanie 16.
126Zadanie 17.
126Zadanie 18.
126Zadanie 19.
126Zadanie 11.
128Zadanie 12.
128Zadanie 13.
128Zadanie 14.
128Zadanie 15.
128Zadanie 16.
128Zadanie 17.
128Zadanie 18.
129Zadanie 19.
129Zadanie 25.
129Zadanie 26.
129Zadanie 27.
129
