Dwusieczne kątów w trójkącie przecinają się w jednym punkcie.
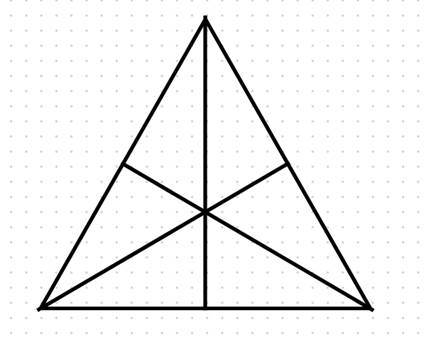

Aby skonstruować dwusieczne kątów trójkąta:
1. Narysuj trójkąt ABC. Zacznij od narysowania danego trójkąta ABC na kartce lub płaszczyźnie.
2. Dla kąta A. Używając cyrkla, umieść jego punkt wierzchołka na wierzchołku kąta A i narysuj łuk, który przecina jedno z ramion kąta (na przykład AB). Następnie umieść końcówkę cyrkla na wierzchołku kąta A i narysuj inny łuk, który przecina drugie ramię kąta (na przykład AC). Punkt przecięcia tych dwóch łuków oznacz jako D. Linia AD będzie jedną z dwusiecznych kąta A.
3. Dla kąta B. Podobnie jak w kroku 2 użyj cyrkla, umieść jego punkt wierzchołka na wierzchołku kąta B i narysuj łuki przecinające ramiona kąta B. Punkty przecięcia tych łuków oznacz jako E. Linia BE będzie jedną z dwusiecznych kąta B.
4. Dla kąta C. Analogicznie użyj cyrkla, umieść jego punkt wierzchołka na wierzchołku kąta C i narysuj łuki przecinające ramiona kąta C. Punkty przecięcia tych łuków oznacz jako F. Linia CF będzie jedną z dwusiecznych kąta C.