W tym zadaniu musisz uzasadnić, że naprzeciwko siebie występują boki równoległe oraz o tej samej długości.
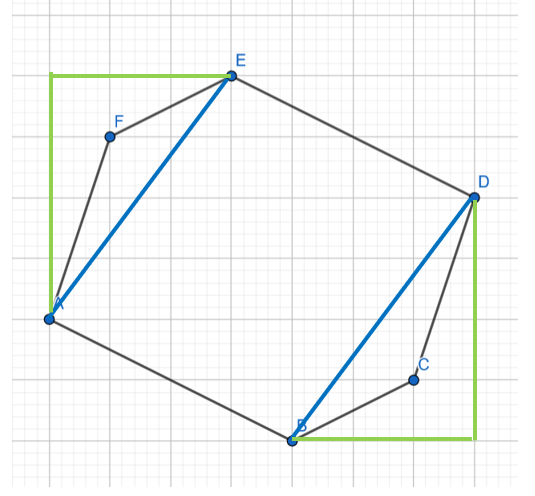
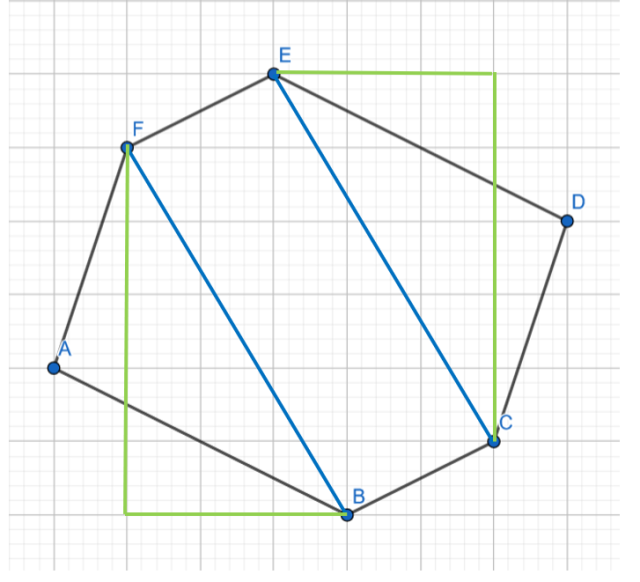
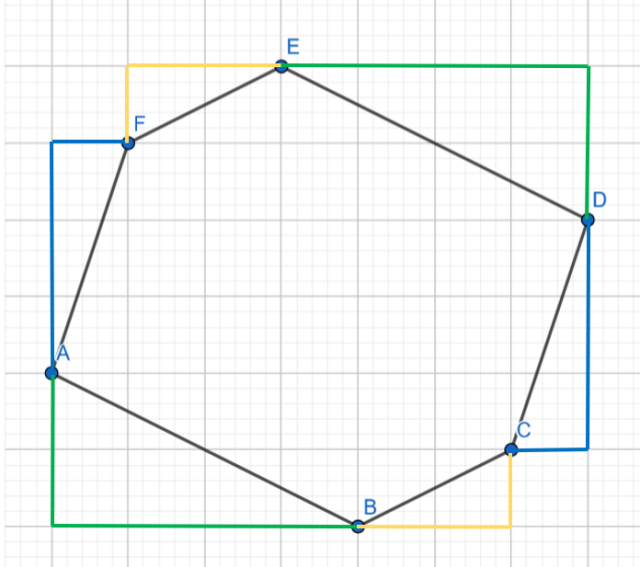
Dwa odcinki są równoległe, jeżeli odległości pomiędzy dwoma punktami są równe. Odległości zaznaczono na rysunkach kolorem jasnoniebieskim. Kolorem jasnozielonym dorysowano na równi z liniami kratek dwie przyprostokątne. Widać, że długości przyprostokątnych są równe, więc i przeciwprostokątne są równe. Na ostatnim rysunku trzema kolorami narysuj przyprostokątne trójkątów prostokątnych, których przeciwprostokątnymi są boki sześciokąta. Przyprostokątne oznaczone jednym kolorem mają równe długości, więc i ich przeciwprostokątne są równe.

Wykonaj rysunek pomocniczy, następnie według opisanego działania, udowadniamy, że w sześciokącie są trzy pary boków równoległych o równych długościach.

Zadanie 1.
124Zadanie 2.
124Zadanie 4.
124Zadanie 8.
125Zadanie 13.
125Zadanie 5.
127Zadanie 6.
127Zadanie 8.
128Zadanie 9.
128Zadanie 10.
128Zadanie 11.
128Zadanie 12.
128Zadanie 14.
128Zadanie 15.
129Zadanie 17.
129Zadanie 18.
129Zadanie 19.
129Zadanie 20.
129Zadanie 21.
129Zadanie 1.
130Zadanie 2.
130Zadanie 6.
130Zadanie 7.
130Zadanie 10.
131Zadanie 12.
131Zadanie 18.
131Zadanie 20.
132Zadanie 22.
132Zadanie 1.
133Zadanie 2.
133Zadanie 3.
133Zadanie 4.
133Zadanie 5.
133Zadanie 8.
134Zadanie 11.
134Zadanie 13.
134Zadanie 14.
134Zadanie 17.
135Zadanie 22.
135Zadanie 15.
137Zadanie 16.
137Zadanie 17.
137
