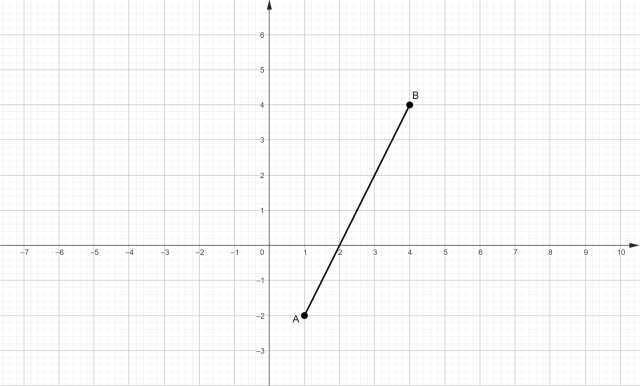
Narysuj wykres funkcji f, która jest odcinkiem o końcach A(1, 2) i B(4, 4). Odczytaj miejsca zerowe, zbiór argumentów oraz, dla których wartości funkcja przyjmuje wartości nieujemne.
m0 = 2
f(x) = ⟨-2; 4⟩
f(x) ![]()
![]()

Zaznacz w układzie współrzędnym podane punkty A oraz B, a następnie je ze sobą połącz, aby utworzyć odcinek. Aby określić zbiór wartości funkcji, sprawdź jej „wysokość”, czyli zakres na osi y, jaki obejmuje. Pamiętaj przy tym, żeby wziąć pod uwagę, czy przedział ma być otwarty czy zamknięty.
f(x) = ⟨-2; 4⟩
Aby określić miejsce zerowe sprawdź, w którym miejscu funkcja przecina oś X i zapisać ten punkty.
m0 = 2
Z kolei, aby sprawdzić, kiedy funkcja przyjmuje wartości nieujemne (czyli równe i większe od zera), sprawdź, dla jakich x, funkcja jest na osi OX lub nad nią i napisz odpowiedni przedział.
f(x) ![]()
![]()

Zadanie Na początek
108Ćwiczenie 1.
109Ćwiczenie 2.
110Ćwiczenie 3.
111Zadanie 1.
111Zadanie 2.
111Zadanie 3.
111Zadanie 4.
111Ćwiczenie 2.
113Zadanie To się liczy!
113Zadanie 1.
114Zadanie 2.
114Zadanie 3.
114Zadanie 4.
114Zadanie 5.
114Zadanie branżowe 6.
114Zadanie branżowe 7.
114Ćwiczenie 2.
116Zadanie To się liczy!
117Ćwiczenie 1.1.
119Ćwiczenie 1.3.
119Ćwiczenie 2.
120Ćwiczenie 3.
120Ćwiczenie 4.
122Zadanie 1.
123Zadanie 2.
123Ćwiczenie 1.
124Ćwiczenie 2.
125Zadanie 1.
125Zadanie 2.
125Ćwiczenie 1.
127Ćwiczenie 2.
127Ćwiczenie 4.
129Ćwiczenie 5.
130Zadanie branżowe 2.
130Zadanie branżowe 3.
130Zadanie Na początek
131Ćwiczenie 1.
131Ćwiczenie 2.
132Ćwiczenie 3.
133Ćwiczenie 4.
134Zadanie 1.
134Zadanie 2.
135Zadanie branżowe 3.
135Zadanie branżowe 4.
135Ćwiczenie 2.
137Zadanie 1.
138Zadanie 2.
138Ćwiczenie 2.
140Zadanie 1.
141Zadanie 2.
141Ćwiczenie 1.1.
143Ćwiczenie 1.2.
143Ćwiczenie 2.2.
145Zadanie 1.
145Zadanie 2.
145Ćwiczenie 1.
146Zadanie branżowe 4.
147Zadanie 4.
148Zadanie 5.
148Zadanie 3.
149Zadanie 6.
149
