Zapisz układ dwóch równań z dwiema niewiadomymi, którego interpretację graficzną przedstawia poniższy rysunek oraz podaj jego rozwiązanie.
![]()
![]()
![]()
![]()
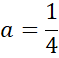
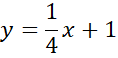
![]()
![]()
![]()
![]()
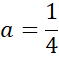
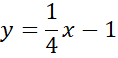
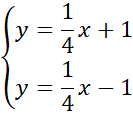
Brak rozwiązania.

Zauważ, że współrzędne punktu przecinającego oś OY dowolnej funkcji wynoszą
![]() oraz że druga współrzędna tego punktu jest równa wyrazowi wolnemu – współczynnikowi
oraz że druga współrzędna tego punktu jest równa wyrazowi wolnemu – współczynnikowi
![]() we wzorze funkcji
we wzorze funkcji
![]() Dodatkowo odczytaj z wykresu inny punkt, który należy do prostej
Dodatkowo odczytaj z wykresu inny punkt, który należy do prostej
![]() . Podstaw jego współrzędne oraz wartość współczynnika
. Podstaw jego współrzędne oraz wartość współczynnika
![]() pod powyższe równanie, aby wyznaczyć współczynnik
pod powyższe równanie, aby wyznaczyć współczynnik
![]() . Następnie zapisz wzór szukanej prostej dla wyznaczonych współczynników.
. Następnie zapisz wzór szukanej prostej dla wyznaczonych współczynników.
W podobny sposób wyznacz wzór prostej
![]() i oba równania zapisz w układzie równań.
i oba równania zapisz w układzie równań.
Na koniec odczytaj z rysunku i zapisz współrzędne przecięcia obu wykresów, czyli rozwiązanie uzyskanego układu równań.

Zadanie 1
210Zadanie 2
210Zadanie 3
210Zadanie 5
211Zadanie 6
211Zadanie 9
211Zadanie 1
215Zadanie 2
215Zadanie 3
216Zadanie 4
216Zadanie 5
216Zadanie 6
216Zadanie 1
220Zadanie 2
220Zadanie 3
220Zadanie 4
220Zadanie 5
220Zadanie 6
221Zadanie 7
221Zadanie 8
221Zadanie 9
221Zadanie 10
221Zadanie 11
221Zadanie 1
224Zadanie 2
224Zadanie 3
225Zadanie 4
225Zadanie 5
225Zadanie 6
225Zadanie 11
234Zadanie 12
234Zadanie 13
234Zadanie 14
234
