Wyznacz współrzędne punktu C, jeśli wykresy funkcji liniowych
oraz
przecinają się w tym punkcie oraz wykres funkcji
przechodzi przez punkty A(2018, -1000) i B(4, 7),
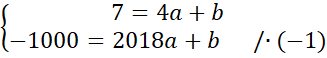
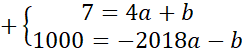
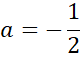
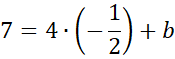
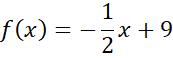
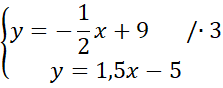
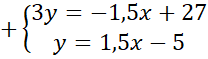
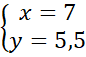
Na początku wyznacz wzór funkcji
. Aby to zrobić współrzędne A i B podstaw pod równanie kierunkowe funkcji liniowej:
. Zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Całe drugie równanie pomnóż przez (-1), aby współczynniki znajdujące się przy
były przeciwne. Dodaj do siebie stronami oba równania znajdujące się w układzie. Z powstałego równania wyznacz wartość
. Wyznaczoną wartość
podstaw pod jedno z początkowych równań i wyznacz z niego wartość
Na koniec zapisz wzór szukanej funkcji.
Następnie zauważ, że punkt przecięcia wykresów obu podanych funkcji jest rozwiązaniem układu równań, którymi są wzory podanych prostych. Całe pierwsze równanie pomnóż przez 3, aby współczynniki znajdujące się przy
były przeciwne. Dodaj do siebie stronami oba równania znajdujące się w układzie. Z powstałego równania wyznacz wartość
. Wyznaczoną wartość
podstaw pod jedno z początkowych równań i wyznacz z niego wartość
