3 = a · (-4) + 2
-4a = 3 – 2
-4a = 1 / :4
![]()
![]()
1 = a · 1 + b
a = 1 – b
2 = a · 2 + b
2 = (1 – b) · 2 + b
2 = 2 – 2b + b
2 – 2 = -2b + b
0 = -b
b = 0
a = 1 – 0 = 1
y = x
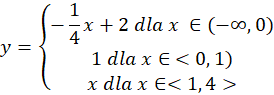

Wzór ogólny funkcji liniowej ma postać: y = ax + b, wiedząc, że funkcja ta przecina oś OY w punkcie (0,2) to współczynnik b = 2. Do wykresu tej funkcji należy punkt A(-4, 3), zatem podstawiając go do wzoru, otrzymasz następujący wzór:
3 = a · (-4) + 2
-4a = 3 – 2
-4a = 1 / :4
![]()
![]()
Wzór ogólny funkcji liniowej ma postać: y = ax + b. Do wykresu tej funkcji należy punkt A(1, 1) oraz B(2, 2), zatem podstawiając go do wzoru, otrzymasz następujący wzór:
1 = a · 1 + b
a = 1 – b
2 = a · 2 + b
2 = (1 – b) · 2 + b
2 = 2 – 2b + b
2 – 2 = -2b + b
0 = -b
b = 0
a = 1 – 0 = 1
y = x