Narysuj równoległobok ABCD i jego dwie przekątne AC i BD. Następnie, oznacz punkt przecięcia tych przekątnych literą S. Wyjaśnij, dlaczego trójkąty ABS i CSD są przystające.
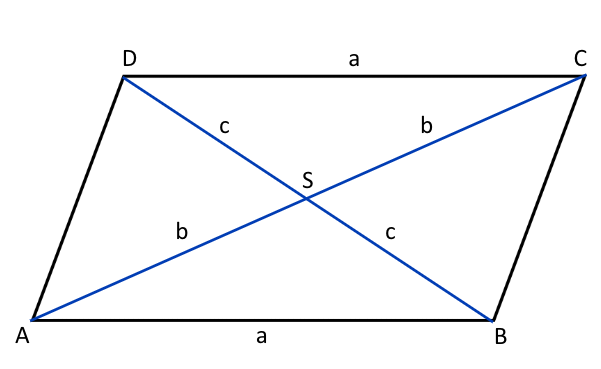

Przekątne równoległoboku przecinają się w połowie, zatem punkt ich przecięcia (S) dzieli obie przekątne na dwa równe odcinki (b i c). Trójkąty ABS oraz CSD mają boki tej samej długości — podstawy równoległoboku są zawsze tej samej długości, są one również podstawami tych trójkątów (a), a ich ramionami są połowy obu przekątnych (b i c). Trójkąty ABS i CSD są zatem przystające, zgodnie z pierwszą cechą przystawania trójkątów (bbb).

Zadanie 3
101Zadanie 4
101Zadanie 7
102Zadanie 8
102Zadanie 11
102Zadanie 12
104Zadanie 2
107Zadanie 3
107Zadanie 4
107Zadanie 5
107Zadanie 9
108Zadanie 10
108Zadanie 11
108Zadanie 13
108Zadanie 15
109Ćwiczenie A
110Ćwiczenie B
110Ćwiczenie C
111Zadanie 1
111Zadanie 3
112Zadanie 5
112Zadanie 9
112Zadanie 11
113Zadanie 12
113Zadanie 1
117Zadanie 3
117Zadanie 4
117Ćwiczenie C
119Zadanie 1
121Zadanie 2
121Zadanie 3
121Zadanie 5
121Zadanie 8
122Zadanie 12
122Zadanie 14
123Ćwiczenie A
124Ćwiczenie C
125Zadanie 6
126Zadanie 7
126Ćwiczenie A
128Zadanie 1
130Zadanie 3
130Zadanie 7
131Zadanie 8
131Zadanie 9
131Zadanie 11
132Zadanie 13
132Zadanie 16
133Zadanie 1
136Zadanie 3
136Zadanie 7
136Zadanie 9
137Zadanie 13
137Zadanie 18
138Zadanie 20
138Zadanie 21
139Zadanie 24
139Zadanie 27
140Ćwiczenie A
141Ćwiczenie B
141Zadanie 3
143Zadanie 6
144Zadanie 7
145Zadanie 10
145Zadanie 1
146Zadanie 3
146Zadanie 4
146Zadanie 6
147Zadanie 3
148Zadanie 4
148Zadanie 5
148Zadanie 6
148Zadanie 7
148Zadanie 11
148Zadanie 12
149Zadanie 13
149Zadanie 18
149Zadanie 26
150Zadanie 27
150Zadanie 29
150Zadanie 30
150Zadanie 31
150Zadanie 32
150Zadanie 34
151Zadanie 39
151Zadanie 47
152Zadanie 49
152Zadanie 52
152Zadanie 53
152
