Wyznacz równanie obrazu okręgu o równaniu
i środku S w skali k=-3.
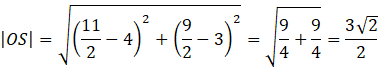
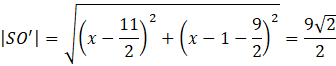
– nie spełnia warunków zadania
ODP:
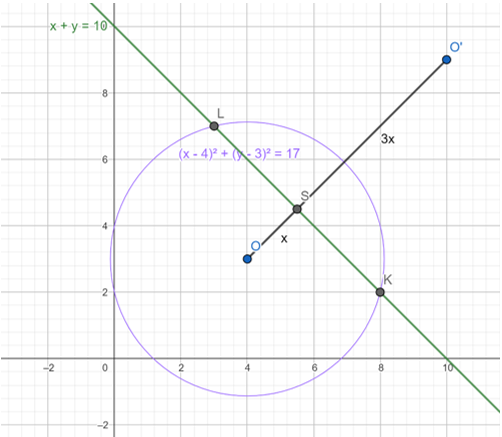
Wykonaj rysunek pomocniczy.
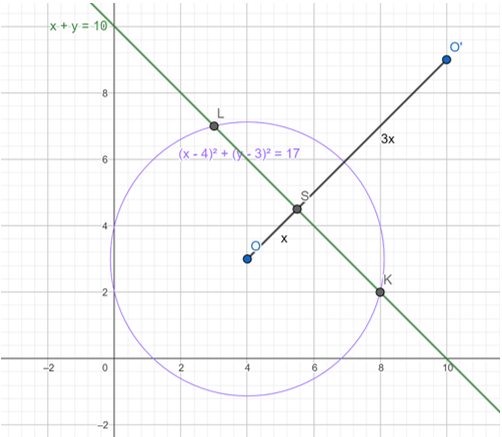
Przekształć równanie okręgu, do uzyskania jego środka i promienia.
Skorzystaj ze wzoru skróconego mnożenia na kwadrat sumy.
Zauważ, że prosta
przecina okrąg w dwóch miejscach. Zapisz równanie okręgu i prostej i rozwiąż układ równań, aby wyznaczyć współrzędne punktów przecięcia.
Skorzystaj z metody podstawienia.
Zauważ, że powstało równanie kwadratowe. Oblicz deltę i miejsca zerowe.
Otrzymane rozwiązania to punkty przecięcia prostej i okręgu. Czyli punkty K i L.
Oblicz współrzędne środka S odcinka KL.
Oblicz długość odcinka OS.
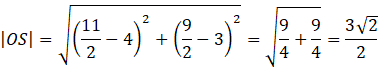
Zauważ, że odcinek SO’ jest trzy razy dłuższy od odcinka SO (skala k=-3).
Aby znaleźć współrzędną punktu O’ wyznacz równanie prostej przechodzącej przez ten punkt. Zauważ, że jest ona prostopadła względem prostej KL i przechodzi przez punkt S.
Współczynnik kierunkowy prostych prostopadłych jest przeciwny i odwrotny.
Wyznacz wartość współczynnika b podstawiając za x i y współrzędne punktu S.
Zapisz współrzędne punktu O’. Pamiętaj, że leży on na prostej OS.
Zauważ, że znasz długość odcinka SO’ i współrzędne punktu S. Korzystając ze wzoru na długość odcinka możesz obliczyć współrzędne punktu O’.
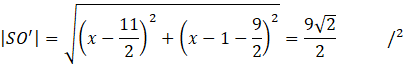
Zauważ, że powstało równanie kwadratowe. Oblicz deltę i miejsca zerowe.
– nie spełnia warunków zadania, ponieważ dla takiego x punkt S nie będzie środkiem jednokładności.
Promień okręgu o środku O’ jest trzy razy dłuższy od promienia okręgu o środku O (skala k=-3).
Pozostało zapisać równanie okręgu o danym środku i promieniu.
