![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ODP.:
![]()

Zauważ, że 2 jest pierwiastkiem wielomianu. Więc
![]() Podstaw te współrzędne w miejsce x i y, aby wyliczyć wartość m.
Podstaw te współrzędne w miejsce x i y, aby wyliczyć wartość m.
![]()
![]()
![]()
![]()
![]()
![]()
Przyrównaj każdą z wartości w nawiasie (również m) do zera, aby wyznaczyć rozwiązania tego równania.
![]()
![]()
Reszta z dzielenia wielomianu (x+1) jest równa 6. Więc
![]() Podstaw te współrzędne w miejsce x i y, aby wyliczyć wartość m.
Podstaw te współrzędne w miejsce x i y, aby wyliczyć wartość m.
![]()
![]()
![]()
Zauważ, że 1 jest pierwiastkiem tego równania, ponieważ
![]()
![]()
Przyrównaj każdą z wartości w nawiasie do zera, aby wyznaczyć rozwiązania tego równania.
![]()
Oblicz dla jakich m pierwsze równanie jest równe 0.
![]()
![]()
Oblicz dla jakich m drugie równanie jest równe 0.
![]()
Oblicz deltę i miejsca zerowe.
![]()
![]()
![]()
![]()
Wspólne rozwiązanie obu równań jest szukaną wartością m.
![]()
Podstaw m pod równanie wielomianu.
![]()
Rozwiąż nierówność
![]()
![]()
![]()
Zauważ, że 2 jest pierwiastkiem tego równania, ponieważ
![]() .
.
![]()
Przyrównaj każdą z wartości w nawiasie do zera, aby wyznaczyć rozwiązania tego równania.
![]()
Oblicz dla jakich x każde z równań jest równe zero.
![]()
Wylicz deltę i miejsca zerowe.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
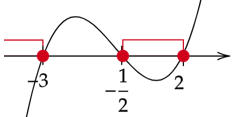
Zaznacz miejsca zerowe na osi, ramiona skieruj w górę, ponieważ współczynnik przy x z najwyższą potęgą jest dodatni. Zaznacz na niej argumenty, dla których wielomian przyjmuje wartości mniejsze lub równe zero, będzie to rozwiązanie nierówności.
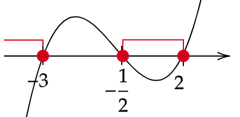
Zapisz przedział rozwiązań nierówności.
![]()