W tym zadaniu musisz obliczyć granice ciągu na podstawie definicji.
Niech
![]() będzie dowolną liczbą dodatnią. Masz pokazać, że istnieje taka liczba
będzie dowolną liczbą dodatnią. Masz pokazać, że istnieje taka liczba
![]() , że wszystkie wyrazy ciągu o numerach większych od
, że wszystkie wyrazy ciągu o numerach większych od
![]() spełniają nierówność
spełniają nierówność
![]() . Mamy:
. Mamy:
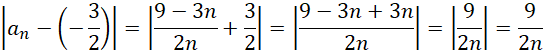
Zauważ, że dla dowolnej liczby naturalnej
![]() otrzymasz:
otrzymasz:
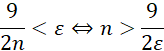
Jeśli dla każdej liczby dodatniej
![]() przyjmiesz
przyjmiesz
![]() , to dla dowolnej liczby naturalnej n większej od
, to dla dowolnej liczby naturalnej n większej od
![]() otrzymasz:
otrzymasz:
![]() , co kończy dowód.
, co kończy dowód.

Liczba g jest granicą nieskończonego ciągu
![]() wtedy i tylko wtedy, gdy dla każdej liczby dodatniej
wtedy i tylko wtedy, gdy dla każdej liczby dodatniej
![]() istnieje taka liczba
istnieje taka liczba
![]() , że dla każdej liczby naturalnej
, że dla każdej liczby naturalnej
![]() większej od
większej od
![]() spełniona jest nierówność
spełniona jest nierówność
![]() .
.

Zadanie 1.
78Zadanie 2.
78Zadanie 4.
78Zadanie 5.
78Zadanie 6.
78Zadanie 8.
79Zadanie 11.
79Zadanie 12.
79Zadanie 13.
79Zadanie 14.
79Zadanie 15.
79Zadanie 1.
84Zadanie 2.
84Zadanie 3.
84Zadanie 4.
84Zadanie 5.
84Zadanie 6.
84Zadanie 7.
84Ćwiczenie 1.
85Ćwiczenie 2.
85Ćwiczenie 3.
86Zadanie 1.
90Zadanie 2.
90Zadanie 3.
91Zadanie 4.
91Zadanie 8.
91Zadanie 9.
91Zadanie 15.
92Zadanie 1.
98Zadanie 2.
98Zadanie 3.
98Zadanie 4.
98Zadanie 5.
98Zadanie 8.
99Zadanie 14.
99Zadanie 15.
99Zadanie 19.
99Ćwiczenie 1.
100Zadanie 1.
107Zadanie 2.
107Zadanie 3.
108Zadanie 5.
108Zadanie 8.
108Zadanie 11.
108Zadanie 16.
109Zadanie 19.
109Zadanie 3.
115Zadanie 6.
116Zadanie 7.
116Zadanie 10.
116Ćwiczenie 1.
122Zadanie 1.
129Zadanie 3.
129Zadanie 4.
129Zadanie 6.
129Zadanie 10.
130Zadanie 11.
130Ćwiczenie 3.
134Zadanie 3.
137Zadanie 7.
137Zadanie 8.
137Ćwiczenie 2.
140Ćwiczenie 3.
142Ćwiczenie 4.
143Zadanie 1.
143Zadanie 2.
143Zadanie 3.
143Zadanie 4.
144Zadanie 5.
144Zadanie 6.
144Zadanie 7.
144Zadanie 8.
144Ćwiczenie 3.
148Zadanie 1.
149Zadanie 2.
148Zadanie 3.
149Ćwiczenie 1.
152Ćwiczenie 4.
154Ćwiczenie 5.
154Zadanie 1.
155Zadanie 2.
155Zadanie 3.
155Zadanie 4.
155Zadanie 5.
155Zadanie 6.
155Ćwiczenie 1.
159Zadanie 1.
161Zadanie 2.
161Zadanie 7.
162Zadanie 8.
162Zadanie 9.
162Zadanie 9.
164Zadanie 10.
164Zadanie 11.
164Zadanie 15.
164Zadanie 17.
165Zadanie 19.
165Zadanie 20.
165
