W tym zadaniu musisz wykazać, że ciąg jest geometryczny.
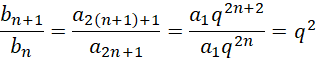
Skoro ciąg
![]() jest ciągiem geometrycznym, to z powyższego równania wynika, że ciąg
jest ciągiem geometrycznym, to z powyższego równania wynika, że ciąg
![]() też jest o stałym ilorazie równym
też jest o stałym ilorazie równym
![]() .
.

Ciąg liczbowy nazywamy ciągiem geometrycznym wtedy i tylko wtedy, gdy iloraz dowolnego wyrazu ciągu i wyrazu bezpośrednio go poprzedzającego jest stały dla danego ciągu.

Zadanie 1.
78Zadanie 2.
78Zadanie 4.
78Zadanie 5.
78Zadanie 6.
78Zadanie 8.
79Zadanie 11.
79Zadanie 12.
79Zadanie 13.
79Zadanie 14.
79Zadanie 15.
79Zadanie 1.
84Zadanie 2.
84Zadanie 3.
84Zadanie 4.
84Zadanie 5.
84Zadanie 6.
84Zadanie 7.
84Ćwiczenie 1.
85Ćwiczenie 2.
85Ćwiczenie 3.
86Zadanie 1.
90Zadanie 2.
90Zadanie 3.
91Zadanie 4.
91Zadanie 8.
91Zadanie 9.
91Zadanie 15.
92Zadanie 1.
98Zadanie 2.
98Zadanie 3.
98Zadanie 4.
98Zadanie 5.
98Zadanie 8.
99Zadanie 14.
99Zadanie 15.
99Zadanie 19.
99Ćwiczenie 1.
100Zadanie 1.
107Zadanie 2.
107Zadanie 3.
108Zadanie 5.
108Zadanie 8.
108Zadanie 11.
108Zadanie 16.
109Zadanie 19.
109Zadanie 3.
115Zadanie 6.
116Zadanie 7.
116Zadanie 10.
116Ćwiczenie 1.
122Zadanie 1.
129Zadanie 3.
129Zadanie 4.
129Zadanie 6.
129Zadanie 10.
130Zadanie 11.
130Ćwiczenie 3.
134Zadanie 3.
137Zadanie 7.
137Zadanie 8.
137Ćwiczenie 2.
140Ćwiczenie 3.
142Ćwiczenie 4.
143Zadanie 1.
143Zadanie 2.
143Zadanie 3.
143Zadanie 4.
144Zadanie 5.
144Zadanie 6.
144Zadanie 7.
144Zadanie 8.
144Ćwiczenie 3.
148Zadanie 1.
149Zadanie 2.
148Zadanie 3.
149Ćwiczenie 1.
152Ćwiczenie 4.
154Ćwiczenie 5.
154Zadanie 1.
155Zadanie 2.
155Zadanie 3.
155Zadanie 4.
155Zadanie 5.
155Zadanie 6.
155Ćwiczenie 1.
159Zadanie 1.
161Zadanie 2.
161Zadanie 7.
162Zadanie 8.
162Zadanie 9.
162Zadanie 9.
164Zadanie 10.
164Zadanie 11.
164Zadanie 15.
164Zadanie 17.
165Zadanie 19.
165Zadanie 20.
165
