Wyznacz równanie kierunkowe prostej, która zawiera dwusieczną kąta ostrego, zawartego między prostymi o równaniach ![]()
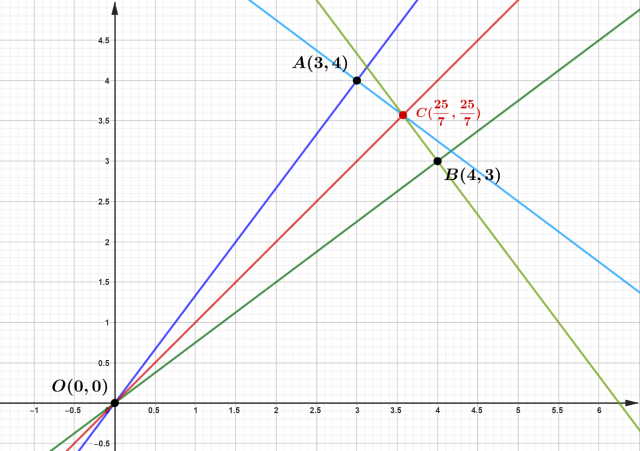
Wskazane proste:
![]()
![]()
Punkty, przez które przechodzą wskazane proste:
![]()
![]()
Proste do nich równoległe:
![]()
![]()
Punkt przecięcia tych prostych:
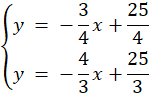
![]()
![]()
![]()
![]()
![]()
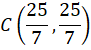
Dwusieczna:
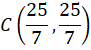
![]()
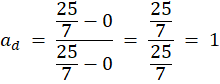
![]()
Dwusieczna to prosta o równaniu ![]()

We wspólnym układzie współrzędnych poprowadź wskazane proste. Następnie wyznacz do nich proste prostopadłe. W tym celu wyznacz punkty kratowe znajdujące się na tych prostych. Z warunku prostopadłości wiadomo, że ich współczynniki są przeciwnymi odwrotnościami do współczynników odpowiednich funkcji liniowych. Kolejno wyznacz punkt wspólny nowych funkcji. Jest on równoodległy od zadanych prostych, więc znajduje się na dwusiecznej kąta zawartego między nimi. Wyznacz równanie tej prostej, wiedząc, że należy do nich punkt przecięcia tych dwóch funkcji, czyli punkt (0, 0).

Zadanie 4.
276Zadanie 7.
276Zadanie 12.
277Zadanie 13.
277Zadanie 15.
277Zadanie 1.
280Zadanie 4.
280Zadanie 6.
281Zadanie 7.
281Zadanie 12.
281Zadanie 16.
282Zadanie 17.
282Zadanie 18.
282Zadanie 20.
282Zadanie 22.
283Zadanie 28.
283Zadanie 29.
284Zadanie 30.
284Zadanie 31.
284Zadanie 32.
284Zadanie 1.
285Zadanie 2.
285Zadanie 3.
285Zadanie 4.
285Zadanie 17.
287Zadanie 22.
288Zadanie 4.
289Zadanie 5.
289Zadanie 12.
290Zadanie 16.
291Zadanie 27.
292Zadanie 2.
293Zadanie 3.
293Zadanie 7.
294Zadanie 11.
294Zadanie 13.
294Zadanie 18.
295Zadanie 19.
295Zadanie 24.
296Zadanie 25.
296Zadanie 27.
296Zadanie 1.
297Zadanie 2.
297Zadanie 4.
297Zadanie 15.
298Zadanie 17.
298Zadanie 20.
299Zadanie 1.
300Zadanie 3.
300Zadanie 9.
300Zadanie 11.
301Zadanie 16.
301Zadanie 26.
302Zadanie 27.
302Zadanie 1.
304Zadanie 2.
304Zadanie 3.
304Zadanie 6.
304Zadanie 7.
304Zadanie 9.
304Zadanie 15.
305Zadanie 24.
306Zadanie 25.
306Zadanie 30.
307
