Udowodnij, że czworokąt EFGH, którego wierzchołki są punktami przecięcia się odcinków łączących wierzchołki kwadratu ABCD ze środkami jego boków o długości a. Następnie wyznacz jego pole.
T : EFGH ∼ ABCD
D :
□ABCD – kwadrat ⇒ |AB| = |BC| = |CD| = |DA| = a
P, Q, R, S – środki boków AB, BC, CD, DA ⇒ |AP| = |BQ| = |CR| = |DS| = 0,5a
⇓ bkb
△ABQ ≡△BCR ≡△CDS ≡△DAP
⇓
|∢QAB| = |∢RBC| = |∢SCD| = |∢PDA| = 𝛼
|∢AQB| = |∢BRC| = |∢CSD| = |∢DPA| = β
𝛼 + β = 90°
⇓
|∢DES| = |∢AFP| = |∢BGQ| = |∢CHR| = 180° - (𝛼 + β) = 90°
Kąty wierzchołkowe:
|∢HEF| = |∢EFG| = |∢FGH| = |∢GHE| = 90°
⇓
▭EFGH – prostokąt
△APF ≡△BQG ≡△CRH ≡△DSE (kbk)
⇓
|FG| = |GH| = |HE| = |EF| = (|AQ| - |AF| - |SF|)
⇓
□EFGH – kwadrat
∎
Twierdzenie Pitagorasa w △ABQ:
![]()
![]()
![]()
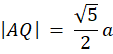
△APF ∼ △ABQ
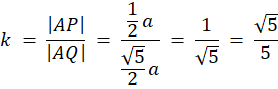
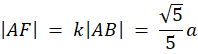
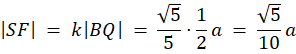
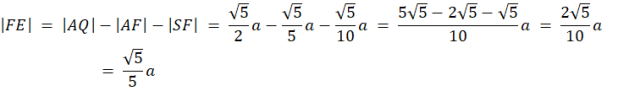
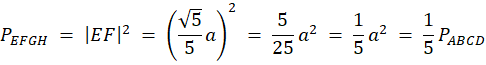

Z twierdzenia Pitagorasa wyznacz długość AQ. Następnie zauważ, że na mocy cechy kkk trójkąty APF i ABQ są podobne. Wyznacz skalę ich podobieństwa (k) jako stosunek długości ich przeciwprostokątnych. Dzięki tej skali oblicz brakujące długości boków trójkąta AFP. Kolejno wyznacz długość boku kwadratu EFGH i oblicz jego pole.

Zadanie 4.
276Zadanie 7.
276Zadanie 12.
277Zadanie 13.
277Zadanie 15.
277Zadanie 1.
280Zadanie 4.
280Zadanie 6.
281Zadanie 7.
281Zadanie 12.
281Zadanie 16.
282Zadanie 17.
282Zadanie 18.
282Zadanie 20.
282Zadanie 22.
283Zadanie 28.
283Zadanie 29.
284Zadanie 30.
284Zadanie 31.
284Zadanie 32.
284Zadanie 1.
285Zadanie 2.
285Zadanie 3.
285Zadanie 4.
285Zadanie 17.
287Zadanie 22.
288Zadanie 4.
289Zadanie 5.
289Zadanie 12.
290Zadanie 16.
291Zadanie 27.
292Zadanie 2.
293Zadanie 3.
293Zadanie 7.
294Zadanie 11.
294Zadanie 13.
294Zadanie 18.
295Zadanie 19.
295Zadanie 24.
296Zadanie 25.
296Zadanie 27.
296Zadanie 1.
297Zadanie 2.
297Zadanie 4.
297Zadanie 15.
298Zadanie 17.
298Zadanie 20.
299Zadanie 1.
300Zadanie 3.
300Zadanie 9.
300Zadanie 11.
301Zadanie 16.
301Zadanie 26.
302Zadanie 27.
302Zadanie 1.
304Zadanie 2.
304Zadanie 3.
304Zadanie 6.
304Zadanie 7.
304Zadanie 9.
304Zadanie 15.
305Zadanie 24.
306Zadanie 25.
306Zadanie 30.
307
