W tym zadaniu musisz obliczyć, na ile sposobów możesz wybrać dwa wierzchołki sześciokąta foremnego o boku długości 1, którego końce są odcinkiem o długości 2.
![]()

Wykonaj rysunek poglądowy:
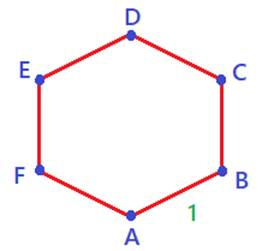
ABCDEF — sześciokąt foremny
![]()
UWAGA:
Analiza zadania przebiega stosując, następujące zależności np.
![]() jest to ten sam odcinek. Czyli kolejność (wybór) wierzchołków nie ma znaczenia.
jest to ten sam odcinek. Czyli kolejność (wybór) wierzchołków nie ma znaczenia.
Wierzchołki {A, B, C, D, E, F}
Wybierz dwa wierzchołki z 6, jest to możliwe na
![]() sposoby, zatem:
sposoby, zatem:
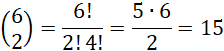
Teraz należy zauważyć (policzyć), ile odcinków o długości 2 ma ten sześciokąt foremny. Pamiętasz, że sześciokąt foremny „zbudowany” jest z sześciu przystających trójkątów równobocznych. Zobacz to na rysunku:

Zatem odcinki o długości 2 o początku i końcu w wierzchołkach tego sześciokąta foremnego „przebiegają” przez boki trójkątów równobocznych. Zatem odcinki o długości 2, to odcinek
![]() . Te odcinki możesz wybrać na 3 sposoby spośród 15 możliwych.
. Te odcinki możesz wybrać na 3 sposoby spośród 15 możliwych.

Zadanie 2.
171Zadanie 3.
171Zadanie 6.
171Zadanie 7.
171Zadanie 8.
171Zadanie 9.
172Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 14.
172Zadanie 1.
178Zadanie 2.
178Zadanie 3.
178Zadanie 4.
178Zadanie 5.
178Zadanie 6.
178Zadanie 7.
178Ćwiczenie 2.
181Ćwiczenie 3.
182Zadanie 1.
184Zadanie 2.
184Zadanie 3.
184Zadanie 4.
184Zadanie 5.
184Zadanie 7.
184Zadanie 9.
185Zadanie 10.
185Zadanie 11.
185Zadanie 12.
185Zadanie 13.
185Ćwiczenie 1.
186Ćwiczenie 4.
188Zadanie 6.
192Zadanie 7.
192Zadanie 8.
192Zadanie 10.
192Zadanie 14.
193Zadanie 15.
193Zadanie 16.
193Zadanie 17.
193Zadanie 18.
193Zadanie 19.
193Zadanie 2.
199Zadanie 3.
199Zadanie 4.
200Zadanie 5.
200Zadanie 6.
200Zadanie 7.
200Zadanie 8.
200Zadanie 12.
200Zadanie 13.
200Ćwiczenie 2.
204Ćwiczenie 5.
205Zadanie 6.
206Zadanie 7.
207Zadanie 8.
207Zadanie 9.
207Zadanie 10.
207Zadanie 15.
207Zadanie 11.
209Zadanie 12.
209Zadanie 13.
209Zadanie 14.
209Zadanie 15.
209Zadanie 16.
209Zadanie 17.
209Zadanie 18.
210Zadanie 19.
210Zadanie 25.
210Zadanie 26.
210Zadanie 27.
210Zadanie 28.
211Zadanie 30.
211Zadanie 32.
211Zadanie 33.
211
