W tym zadaniu musisz obliczyć miary kątów ostrych trójkąta oraz obliczyć stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu opisanego na tym trójkącie.
![]()

Oznacz przyprostokątne jako
![]() i
i
![]() oraz promień okręgu wpisanego w ten trójkąt jako
oraz promień okręgu wpisanego w ten trójkąt jako
![]() . Wtedy przeciwprostokątna
. Wtedy przeciwprostokątna
![]() może być wyrażona za pomocą wzoru:
może być wyrażona za pomocą wzoru:
![]()
![]()
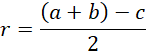
Promień okręgu opisanego na tym trójkącie oznacz jako
![]() , wtedy:
, wtedy:
![]()
![]()
Stosunek długości promienia okręgu wpisanego do opisanego na tym trójkącie wyniesie:
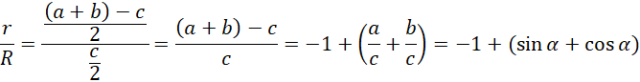
Korzystasz tutaj z faktu, że stosunek przyprostokątnej do przeciwprostokątnej można wyrazić za pomocą odpowiednich funkcji trygonometrycznych.
Zdefiniuj funkcje:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Czyli kąty ostre w tym trójkącie wyniosą:
![]()
A stosunek wyniesie:
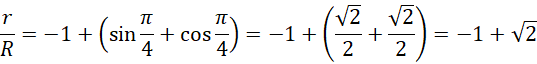

Ćwiczenie 6.
392Ćwiczenie 9.
395Zadanie 1.
396Zadanie 2.
396Zadanie 3.
396Zadanie 4.
396Zadanie 5.
397Zadanie 6.
397Zadanie 8.
397Zadanie 9.
397Zadanie 10.
397Zadanie 1.
401Zadanie 2.
401Zadanie 3.
401Zadanie 4.
401Ćwiczenie 3.
404Ćwiczenie 4.
406Zadanie 1.
409Zadanie 2.
409Zadanie 3.
409Zadanie 4.
409Zadanie 5.
409Zadanie 6.
409Zadanie 7.
410Zadanie 8.
410Zadanie 9.
410Zadanie 10.
410Zadanie 11.
410Zadanie 12.
410Zadanie 13.
410Ćwiczenie 1.
414Ćwiczenie 4.
417Zadanie 1.
418Zadanie 2.
418Zadanie 3.
419Zadanie 4.
419Zadanie 5.
419Zadanie 6.
419Zadanie 7.
419Zadanie 11.
419Ćwiczenie 1.
421Zadanie 1.
423Zadanie 2.
423Zadanie 3.
424Zadanie 4.
424Zadanie 9.
424Zadanie 10.
424Zadanie 1.
428Zadanie 3.
429Zadanie 5.
429Zadanie 6.
429Zadanie 8.
429Zadanie 1.
434Zadanie 2.
435Zadanie 3.
435Zadanie 4.
435Zadanie 5.
435Ćwiczenie 1.
437Zadanie 1.
440Zadanie 2.
441Zadanie 3.
441Zadanie 4.
441Zadanie 5.
441Zadanie 8.
441Ćwiczenie 1.
442Zadanie 1.
448Zadanie 2.
448Zadanie 10.
450Zadanie 11.
450Zadanie 12.
450Zadanie 13.
450Zadanie 14.
450
