W tym zadaniu musisz wyznaczyć parametr, dla którego dane równanie trygonometryczne ma rozwiązanie.
![]()

![]()
Skorzystaj ze wzoru na sumę cosinusów:
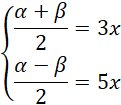
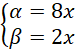
Stąd:
![]()
![]()
![]()
Rozwiązanie istnieje wtedy i tylko wtedy, gdy:
![]()
![]()
![]()
![]()
![]()
Biorąc część wspólną policzonych zbiorów, dostaniesz:
![]()

Ćwiczenie 6.
392Ćwiczenie 9.
395Zadanie 1.
396Zadanie 2.
396Zadanie 3.
396Zadanie 4.
396Zadanie 5.
397Zadanie 6.
397Zadanie 8.
397Zadanie 9.
397Zadanie 10.
397Zadanie 1.
401Zadanie 2.
401Zadanie 3.
401Zadanie 4.
401Ćwiczenie 3.
404Ćwiczenie 4.
406Zadanie 1.
409Zadanie 2.
409Zadanie 3.
409Zadanie 4.
409Zadanie 5.
409Zadanie 6.
409Zadanie 7.
410Zadanie 8.
410Zadanie 9.
410Zadanie 10.
410Zadanie 11.
410Zadanie 12.
410Zadanie 13.
410Ćwiczenie 1.
414Ćwiczenie 4.
417Zadanie 1.
418Zadanie 2.
418Zadanie 3.
419Zadanie 4.
419Zadanie 5.
419Zadanie 6.
419Zadanie 7.
419Zadanie 11.
419Ćwiczenie 1.
421Zadanie 1.
423Zadanie 2.
423Zadanie 3.
424Zadanie 4.
424Zadanie 9.
424Zadanie 10.
424Zadanie 1.
428Zadanie 3.
429Zadanie 5.
429Zadanie 6.
429Zadanie 8.
429Zadanie 1.
434Zadanie 2.
435Zadanie 3.
435Zadanie 4.
435Zadanie 5.
435Ćwiczenie 1.
437Zadanie 1.
440Zadanie 2.
441Zadanie 3.
441Zadanie 4.
441Zadanie 5.
441Zadanie 8.
441Ćwiczenie 1.
442Zadanie 1.
448Zadanie 2.
448Zadanie 10.
450Zadanie 11.
450Zadanie 12.
450Zadanie 13.
450Zadanie 14.
450
