W tym zadaniu musisz policzyć cosinus sumy kątów.
![]()

Z jedynki trygonometrycznej dla kąta:
![]()
![]()
![]()
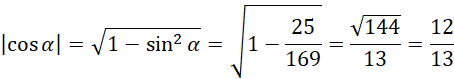
Ponieważ kąt alfa jest w drugiej ćwiartce, cosinus alfa będzie liczbą ujemną:
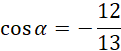
Z tangensa beta:
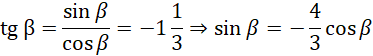
Po podniesieniu do kwadratu:
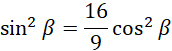
Z jedynki trygonometrycznej dla kąta:
![]()
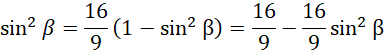
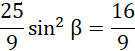
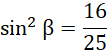
Ponieważ kąt beta jest w czwartej ćwiartce, sinus beta będzie liczbą ujemną:
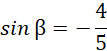
Natomiast cosinus beta będzie liczbą dodatnią:
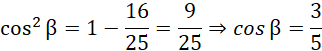
Skorzystaj ze wzory na „cosinus sumy”:
![]()
Podstaw wcześniej wyliczone wyrażenia:
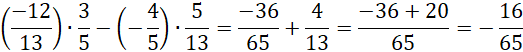

Ćwiczenie 6.
392Ćwiczenie 9.
395Zadanie 1.
396Zadanie 2.
396Zadanie 3.
396Zadanie 4.
396Zadanie 5.
397Zadanie 6.
397Zadanie 8.
397Zadanie 9.
397Zadanie 10.
397Zadanie 1.
401Zadanie 2.
401Zadanie 3.
401Zadanie 4.
401Ćwiczenie 3.
404Ćwiczenie 4.
406Zadanie 1.
409Zadanie 2.
409Zadanie 3.
409Zadanie 4.
409Zadanie 5.
409Zadanie 6.
409Zadanie 7.
410Zadanie 8.
410Zadanie 9.
410Zadanie 10.
410Zadanie 11.
410Zadanie 12.
410Zadanie 13.
410Ćwiczenie 1.
414Ćwiczenie 4.
417Zadanie 1.
418Zadanie 2.
418Zadanie 3.
419Zadanie 4.
419Zadanie 5.
419Zadanie 6.
419Zadanie 7.
419Zadanie 11.
419Ćwiczenie 1.
421Zadanie 1.
423Zadanie 2.
423Zadanie 3.
424Zadanie 4.
424Zadanie 9.
424Zadanie 10.
424Zadanie 1.
428Zadanie 3.
429Zadanie 5.
429Zadanie 6.
429Zadanie 8.
429Zadanie 1.
434Zadanie 2.
435Zadanie 3.
435Zadanie 4.
435Zadanie 5.
435Ćwiczenie 1.
437Zadanie 1.
440Zadanie 2.
441Zadanie 3.
441Zadanie 4.
441Zadanie 5.
441Zadanie 8.
441Ćwiczenie 1.
442Zadanie 1.
448Zadanie 2.
448Zadanie 10.
450Zadanie 11.
450Zadanie 12.
450Zadanie 13.
450Zadanie 14.
450
