W tym zadaniu musisz udowodnić, iż równanie 3x2 + 4x +
![]() = 0, ma miejsca zerowe, które są sinusem i cosinusem pewnego kąta.
= 0, ma miejsca zerowe, które są sinusem i cosinusem pewnego kąta.
3x2 + 4x +
![]() = 0
= 0
3x2 + 4x +
![]() = 0
= 0
∆ = (4)2–4∙3∙
![]()
∆ = 16–14
∆ = 2 | √
√∆ = √2
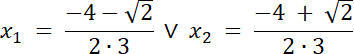
x1 = sin α i x2 = cos α, to: sin2α + cos2α = 1, więc
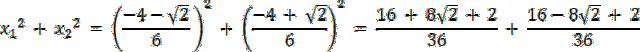
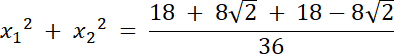
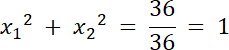

W tym zadaniu musisz najpierw wyznaczyć rozwiązania równania, a następnie udowodnić, że są one odpowiednio sinusem i cosinusem pewnego kąta. Skoro rozwiązania są zarówno sinusem i cosinusem kąta to: sin2α + cos2α = 1, więc sprawdź, czy x12 + x22 = 1.

Ćwiczenie 3.
164Ćwiczenie 4.
164Ćwiczenie 5.
164Ćwiczenie 7.
165Ćwiczenie 9.
166Zadanie 1.
167Zadanie 2.
167Zadanie 3.
167Ćwiczenie 2.
171Zadanie 1.
173Zadanie 2.
174Zadanie 3.
173Zadanie 4.
173Zadanie 5.
173Zadanie 6.
173Zadanie 7.
173Zadanie 8.
173Zadanie 1.
179Zadanie 2.
179Zadanie 3.
180Zadanie 4.
180Zadanie 9.
180Ćwiczenie 4.
185Zadanie 1.
185Zadanie 2.
185Zadanie 3.
185Zadanie 4.
185Zadanie 5.
185Zadanie 6.
185Zadanie 7.
185Zadanie 11.
187Zadanie 18.
187Zadanie 20.
187
