Zadanie
W tym zadaniu musisz wyznaczyć wartość kąta α i narysować ten kąt w układzie współrzędnych, znając wartość dwóch funkcji trygonometrycznych.
Rozwiązanie
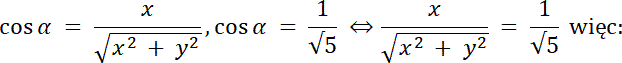
√x2 + y2 = √5, gdzie √x2 + y2 = r–wzór na promień okręgu
x = 1 i tg α > 0, więc kąt znajduje się w I ćwiartce.
Skonstruuj punkt P znajdujący się na drugim ramieniu kąta α, który spełnia trzy warunki:
a) współrzędna x, punktu P: x = 1
b) odległość punktu P od punktu 0 (0,0) jest równa √5
c) tg α > 0
Wyjaśnienie
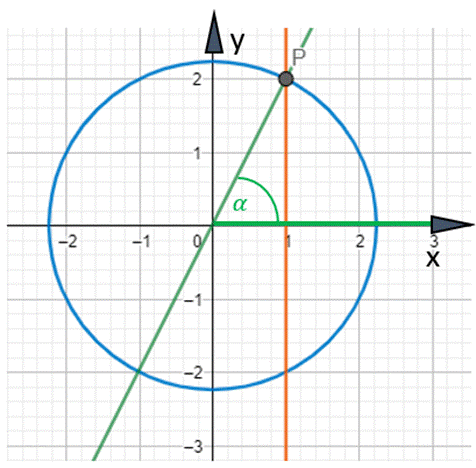
W tym zadaniu skorzystaj ze wzoru na cos α, aby wyznaczyć warunki dla punktu P, przyrównaj liczniki ułamków oraz mianowniki, narysuj odpowiedni wykres i okrąg w układzie współrzędnych. Rozwiązaniem zadania jest tylko jedno miejsce przecięcia osi x = 1 z okręgiem oraz tg α > 0. Punkt, który spełnia wszystkie 3 warunki, znajduje się w I ćwiartce układu współrzędnych.
Matematyka - wybrane pytania
REKLAMA
Zadania z tego działu
Trygonometria
163
Trygonometria–powtórzenie wiadomości z geometrii z klasy 1.
163
Ćwiczenie 3.
164Ćwiczenie 4.
164Ćwiczenie 5.
164Ćwiczenie 7.
165Ćwiczenie 9.
166Zadanie 1.
167Zadanie 2.
167Zadanie 3.
167
Sinus, cosinus, tangens i cotangens dowolnego kąta płaskiego
168
Ćwiczenie 2.
171Zadanie 1.
173Zadanie 2.
174Zadanie 3.
173Zadanie 4.
173Zadanie 5.
173Zadanie 6.
173Zadanie 7.
173Zadanie 8.
173
Podstawowe tożsamości trygonometryczne
175
Zadanie 1.
179Zadanie 2.
179Zadanie 3.
180Zadanie 4.
180Zadanie 9.
180
Wybrane wzory redukcyjne
181
Ćwiczenie 4.
185Zadanie 1.
185Zadanie 2.
185Zadanie 3.
185Zadanie 4.
185Zadanie 5.
185Zadanie 6.
185Zadanie 7.
185
Sprawdź, czy umiesz–powtórzenie rozdziału 5
186
Zadanie 11.
187Zadanie 18.
187Zadanie 20.
187