W tym zadaniu musisz wyznaczyć długość przeciwprostokątnej trójkąta prostokątnego, a następnie wyznaczyć wartości trygonometryczne najmniejszego kąta w tym trójkącie.
c–długość boku przeciwprostokątnej w cm i c > 0
82 + 152 = c2
64 + 225 = c2
c2 = 289⇒ c = 17 cm
α–wartość najmniejszego kąta w trójkącie
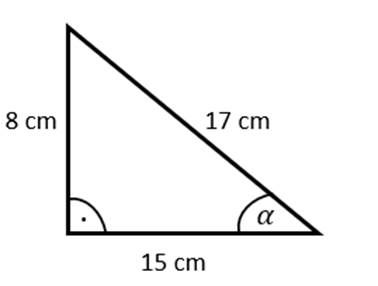
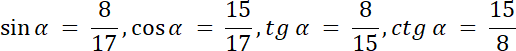

W pierwszym kroku, korzystając z twierdzenia Pitagorasa, musisz wyznaczyć długość przeciwprostokątnej w trójkącie prostokątnym. Najmniejszy kąt w trójkącie znajduje się naprzeciwko najkrótszego boku trójkąta i na tej podstawie wyznaczasz funkcje trygonometryczne: sin α, cos α, tg α, ctg α.

Ćwiczenie 3.
164Ćwiczenie 4.
164Ćwiczenie 5.
164Ćwiczenie 7.
165Ćwiczenie 9.
166Zadanie 1.
167Zadanie 2.
167Zadanie 3.
167Ćwiczenie 2.
171Zadanie 1.
173Zadanie 2.
174Zadanie 3.
173Zadanie 4.
173Zadanie 5.
173Zadanie 6.
173Zadanie 7.
173Zadanie 8.
173Zadanie 1.
179Zadanie 2.
179Zadanie 3.
180Zadanie 4.
180Zadanie 9.
180Ćwiczenie 4.
185Zadanie 1.
185Zadanie 2.
185Zadanie 3.
185Zadanie 4.
185Zadanie 5.
185Zadanie 6.
185Zadanie 7.
185Zadanie 11.
187Zadanie 18.
187Zadanie 20.
187
