c = 15
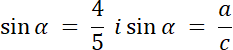
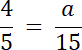
![]()
a = 12
a2 + b2 = c2 |–a2
b2 = (15)2–(12)2
b2 = 225–144
b2 = 81
b = 9 v b = –9,
b < 0–bo szukamy współrzędnej x, w II ćwiartce
współrzędne punktu P: P(–9, 12)

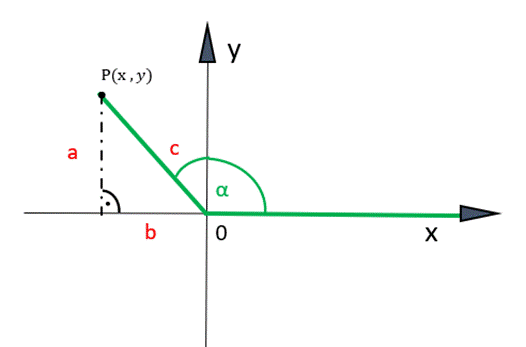
W pierwszym kroku załóż, że kąt α znajduje się w położeniu standardowym, a na drugim ramieniu kąta zaznacz punkt P. Poprowadź linię przerywaną od punktu P, prostopadle do osi OX. Zauważ, że otrzymałeś trójkąt prostokątny, a odległość punktu P od punktu (0,0) stanowi długość przeciwprostokątnej tego trójkąta. Na podstawie wartości sin α, wyznacz długość odcinka a–długość prostopadłej do osi OX, a z twierdzenia Pitagorasa odległość od punktu przecięcia linii z osią OX do punktu początku układu współrzędnych. Zauważ, że punkt P znajduje się w II ćwiartce układu współrzędnych, więc wartość współrzędnej x będzie ujemna. Wartość współrzędnej x–określa długość odcinka b, a wartość współrzędnej y–długość odcinka a.