Zadanie
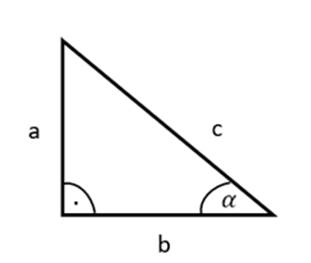
W tym zadaniu musisz narysować kąt ostry α, w trójkącie prostokątnym, jeżeli tg α = 4.
Rozwiązanie
Skoro trójkąt jest prostokątny, to:
a2 + b2 = c2 i a > 0, b > 0, c > 0
(4b)2 + b2 = c2
17b2 = c2
17b = c ∨ 17b = –c, c > 0
17b = c
Boki tego trójkąta: 4b, b, 17b
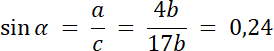
sin α = 0,24 ⇔ α = 14°
Wyjaśnienie
W pierwszym kroku wyznacz, jaka jest zależność między bokami w trójkącie prostokątnym, a następnie z twierdzenia Pitagorasa, wyznacz długość boku przeciwprostokątnej. Otrzymany trójkąt ma boki następującej długości: 4b, b, 17b. Na koniec, skorzystaj z funkcji trygonometrycznej np. sinusa kąta, aby obliczyć dokładna wartość kąta α. Dokładne wartości funkcji trygonometrycznych odczytaj z tabeli i narysuj trójkąt prostokątny, który posiada kąt α.
Matematyka - wybrane pytania
REKLAMA
Zadania z tego działu
Trygonometria
163
Trygonometria–powtórzenie wiadomości z geometrii z klasy 1.
163
Ćwiczenie 3.
164Ćwiczenie 4.
164Ćwiczenie 5.
164Ćwiczenie 7.
165Ćwiczenie 9.
166Zadanie 1.
167Zadanie 2.
167Zadanie 3.
167
Sinus, cosinus, tangens i cotangens dowolnego kąta płaskiego
168
Ćwiczenie 2.
171Zadanie 1.
173Zadanie 2.
174Zadanie 3.
173Zadanie 4.
173Zadanie 5.
173Zadanie 6.
173Zadanie 7.
173Zadanie 8.
173
Podstawowe tożsamości trygonometryczne
175
Zadanie 1.
179Zadanie 2.
179Zadanie 3.
180Zadanie 4.
180Zadanie 9.
180
Wybrane wzory redukcyjne
181
Ćwiczenie 4.
185Zadanie 1.
185Zadanie 2.
185Zadanie 3.
185Zadanie 4.
185Zadanie 5.
185Zadanie 6.
185Zadanie 7.
185
Sprawdź, czy umiesz–powtórzenie rozdziału 5
186
Zadanie 11.
187Zadanie 18.
187Zadanie 20.
187