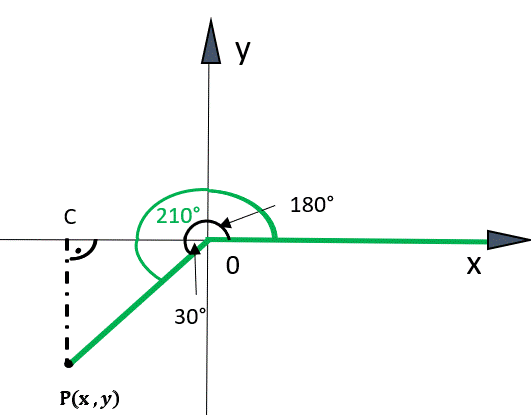
kąt α = 210°, czyli α = 180° + 30°
|∢P0C| = 30° i |∢C0P| = 60°
Trójkąt CPO–trójkąt prostokątny, stanowiący „połowę” trójkąta równobocznego
Punkt C(–1,0), punkt P(x, y)
![]() , gdzie a–długość boku trójkąta równobocznego
, gdzie a–długość boku trójkąta równobocznego
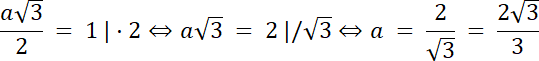
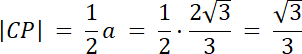
Punkt P znajduje się w III ćwiartce, gdzie x < 0, y < 0, więc:
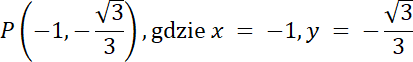
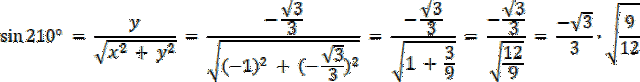
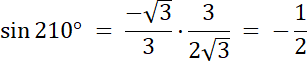
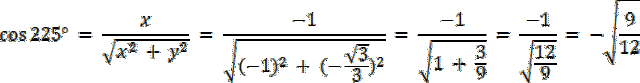
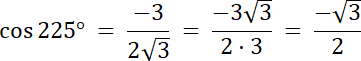
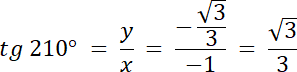
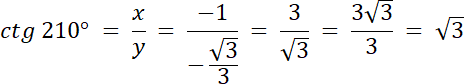

W pierwszym kroku znajdź, w której ćwiartce znajduje się drugie ramię kąta 210°–jest w III ćwiartce układu współrzędnych. Zauważ również, że 210° = 180° + 30°, więc kąt między osią OX, a drugim ramieniem kąta wynosi 30° (zobacz na rysunek w rozwiązaniu). Weź pod uwagę trójkąt CP0, który jest „połową” trójkąta równobocznego. Wiadomo również, że |C0| to wysokość trójkąta równobocznego, więc współrzędna x dla punktu C i punktu P będzie mieć taką sama wartość, a odległość punktu P od C będzie równe połowie długości boku trójkąta. Z wysokości wyznacz długość boku tego trójkąta, a następnie długość boku |CP| i |CP| = |y| Po wyznaczeniu współrzędnych x, y dla punktu P, wyznacz wartości funkcji trygonometrycznych dla kąta 210°, korzystając z definicji, która uwzględnia współrzędne x, y.